metric learning希望使同源的向量相似度尽可能的高，而非同源的向量相似度尽可能的低，即类内相近，类间分离。通过distance metric引导分类器可以学习到能区分不同类的特征组合，所以多被用于 CV 的人脸识别，NLP 的语义匹配等。

在语义模型的训练框架里，Deep Metric Learning 大致可以分为两类：分类和排序。

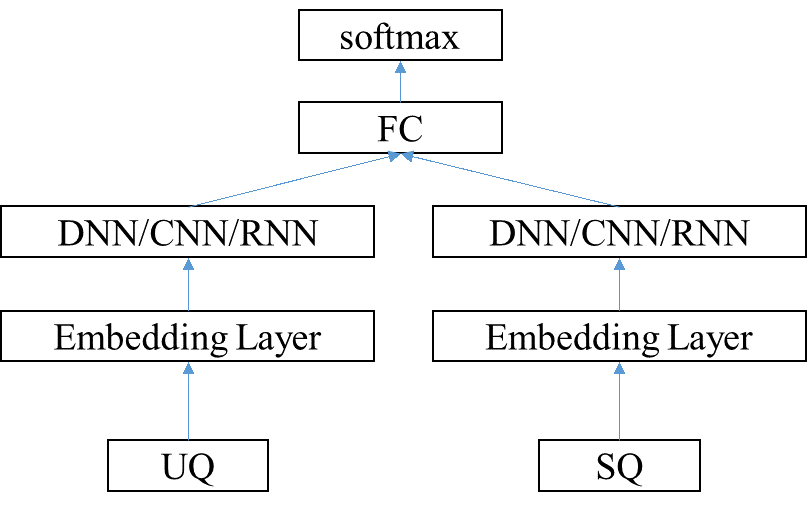
采用分类的方法，一般最后一层接的是多类别的softmax，即输入是用户Q，分类结果是所属的标准Q类别。
排序学习有三种类型：point-wise, pair-wise和list-wise。在QA中我们常用的是point-wise和pair-wise。其中point-wise的方法直接把问题转换成二分类，判断当前用户问题是否属于带匹配的问题，最后根据隶属概率值可以得到问题的排序。而pair-wise学习的是和两两之间的排序关系，训练目标是最大化正样本对和负样本对的距离。

分类的方法	point-wise	pair-wise

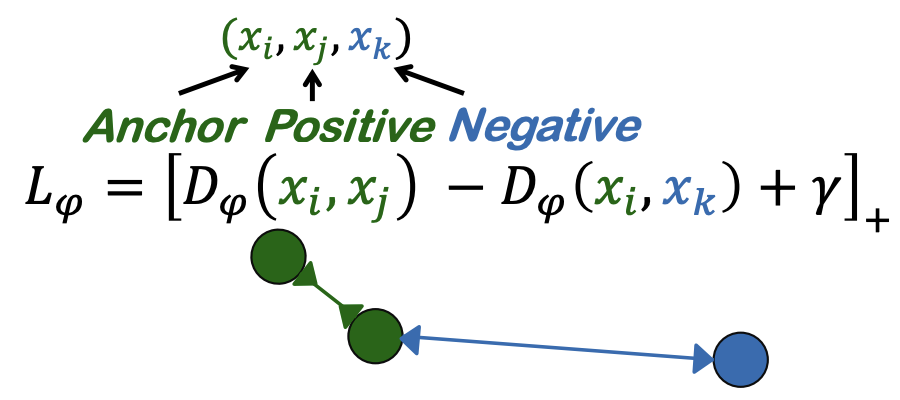
对应损失函数的形式大致如下：

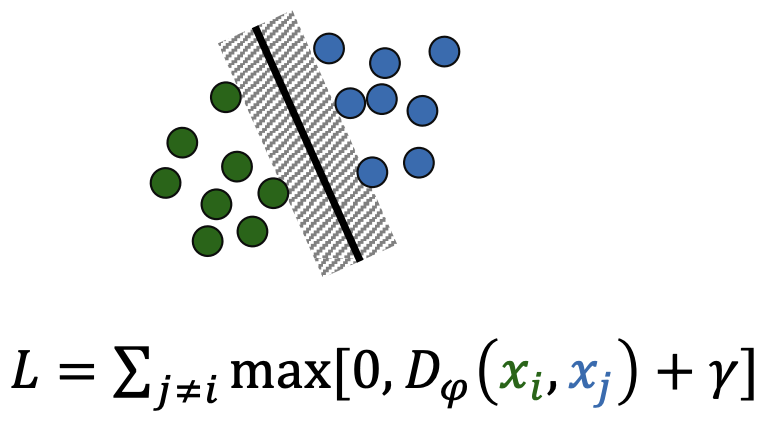Ranking-based Loss

Contrastive loss

想要学习一个pair的相似度，最容易想到的就是把它当作一个分类问题，即同一个人的人脸pair的欧式距离d（a0，a1）作为正例（label=1），不同人的人脸pair（a0，b1）为负例（label=0）。那么如果用经典的二元交叉熵损失如下：

$Loss=-\left(y_{i} \log \hat{y}_{i}+\left(1-y_{i}\right) \log \left(1-\hat{y}_{i}\right)\right)$

cross entropy loss希望正例趋近于1，负例趋近于0。当y=1时，p=1时loss最小；当y=0时，p=0时loss最小。那么我们可以直接把cross entropy中的p替换成距离d吗？不能。原因有三：一是d的值域不属于[0,1]；二是我们的任务中希望y=1时距离d越小越好；三是希望y=0时d越大越好。后两点与cross entropy的优化目标正好相反。因此，需要对loss进行一些改进，例如把log函数改为平方函数：

$Loss=yd^2+(1-y)(1-d^2)$

这样改进之后解决了第二个问题，当y=1时d越小loss越小；但此时y=0时优化的目标是d越接近于1越好，这与我们的任务期待不符，继续改进：

$Loss=yd^2+(1-y)max(margin-d, 0)^2$

其中margin是可根据任务调节的超参数。经过这次改进后，问题一和三也被解决。当y=0时，d的优化目标为比margin大，在某种程度上这个loss通过margin参数达到了“类内相近，类间分离”的作用。这个loss即为contrastive loss，出自Yann LeCun在2015发表的Dimensionality Reduction by Learning an Invariant Mapping，官方的损失公式如下所示：

$L=\frac{1}{2N} \sum_{n=1}^{N}Y\left(D_{W}\right)^{2}+(1-Y)\left\{\max \left(0, margin-D_{W}\right)\right\}^{2}$

$D_{W}\left(\vec{X}_{1}, \vec{X}_{2}\right)=\left|G_{W}\left(\vec{X}_{1}\right)-G_{W}\left(\vec{X}_{2}\right)\right|_{2}=\sqrt{\sum_{i=1}^{n}\left(x_{1i}-x_{2i}\right)^{2}}$

从拓扑的观点来看，Contrastive Loss使得网络学习到一种映射关系(神经网络或转换矩阵)，把向量从原始空间映射到新的空间从而使得向量在新的空间有更好的拓扑性质，即类内尽可能紧凑类间尽可能分离。

Contrastive loss的缺点：尽管它很受欢迎，但在大多数检索任务(通常用作基线)中，这种对比性损失的表现很不起眼。大多数高级损失需要一个三元组$(x_i,x_j,x_k)$，其中$(x_i,x_j)$属于同一类，$(x_i,x_k)$属于不同类。这种三元组样本在无监督学习中很难获得。因此，尽管对比损失在检索方面的表现不佳，但在无监督学习和自监督学习中仍普遍使用。

代码参考1：

def contrastive_loss(y_true, y_pred):
    '''Contrastive loss from Hadsell-et-al.'06
    http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
    '''
    margin = 1
    sqaure_pred = K.square(y_pred)
    margin_square = K.square(K.maximum(margin - y_pred, 0))
    return K.mean(y_true * sqaure_pred + (1 - y_true) * margin_square)

model.compile(loss=contrastive_loss, ...)

代码参考2：

1
2
3

tf.contrib.losses.metric_learning.contrastive_loss(
    labels, embeddings_anchor, embeddings_positive, margin=1.0
)

Triplet loss

参考资料：
Implementing Triplet Loss Function in Tensorflow 2.0
Tensorflow实现Triplet Loss
深度学习从入门到放飞自我：完全解析triplet loss
Triplet Loss and Online Triplet Mining in TensorFlow
triplet loss稳定在margin附近?—hardTri & l2_normalize
为什么triplet loss有效？从直观上说明为什么triplet loss不稳定?

contrastive loss是一个严格的loss，它要求正例距离趋近于0，负例距离大于margin。然而，有一些距离较近的负例，它们的正例也较近；有一些距离较远的负例，它们的正例也较远，统一对待这两种情况，模型可能无法很好的训练。考虑一个正脸的数据集里有一张稍微偏一些的侧脸，如果这张侧脸图片作为contrastive loss中的a0，它的pair的正例/负例距离明显大于其它pair的正例/负例距离。如果它的优化目标和其它pair一样，正例趋近于0，负例大于margin，是不合理的。那么是否有一种没有这么严格的loss呢？有，triplet loss。

Triplet loss 出自2014 年的 FaceNet 论文，经常用在人脸识别任务中，目的是学习度量嵌入（to learn a metric embedding）。它的输入是一个三元组（anchor，positive，negative），具体的loss function为：

$\mathcal{L}_{\mathrm{tri}}^{m}\left(x, x^{+}, x^{-} ; f\right)=\max \left(0,\left|f-f^{+}\right|_{2}^{2}-\left|f-f^{-}\right|_{2}^{2}+m\right)$

triplet loss的优化目标就是让Anchor与负例的欧式比Anchor与正例的距离大至少一个margin。还是以上述的侧脸图片为例，侧脸图片作为anchor时，triplet loss不要求正例趋近于0，负例大于margin，而是负例>正例+margin，这就解决了刚才的问题。当dis(A, N) – dis(A, P) < margin时，loss会大于0。

Triplet Loss 训练过程动图：

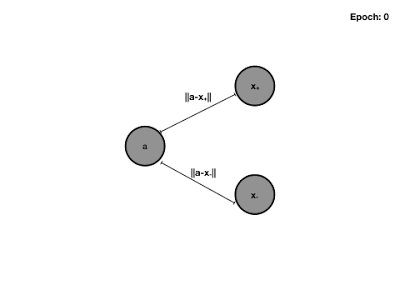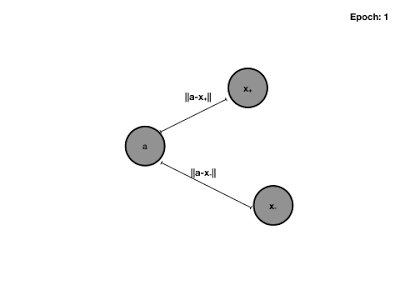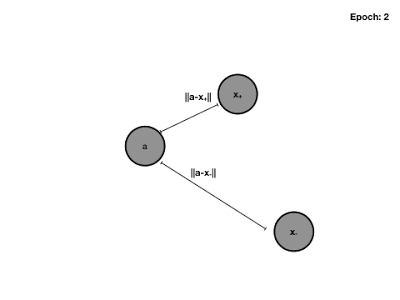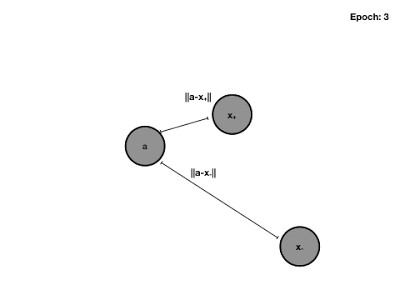
Triplet loss 的不足之处：

Triplet loss 对噪声数据很敏感，因此随机负采样会影响其性能；
Triplet loss 的实现不是很简单，比较tricky的地方是如何计算embedding的距离，以及怎样识别并抛弃掉invalid和easy triplet（需要较好的采样策略）；
Triplet loss 训练过程不稳定，收敛速度慢，需要极大的耐心去调参；
来分析一下为什么单纯使用triplet loss效果不好，我们对比softmax的损失函数以及triplet loss上界版本的损失函数不难发现：softmax损失函数和triplet loss上界版本中，每一个batch的loss都能够兼顾全局的信息，并进行权重更新，这一点能够保证整个训练过程相对平滑稳定。其中softmax是天然如此，而triplet loss上界版则是通过引入centroid实现的。反观原始的triplet loss的形式，每个batch所涉及和更新的信息是非常局限的(只含2个类别)，如果不能设计合理的采样和训练策略，很容易出现的一种情况是某个类别的embedding分布不稳定、出现突变和跃迁，导致训练反复、难以收敛。

分析triplet loss在 hard negtive 下坍塌问题

问题描述：
Triplet models are susceptible to mapping each input to the same point. When this happens, the distances in (*) go to zero the loss gets stuck at a and the model is basically done updating. Semi-hard negative mining can also help prevent this from happening. In my experience, the loss tending towards a is a clear signal that training isn’t working as desired and the embeddings are not informative. You can check whether this is the case by examining the embedding vectors: if the classes tend to be close together, there’s a problem.

分析：

坍塌问题（collapse issue），这意味着所有的句子都倾向于编码到一个较小的局部区域内
为什么triplet loss选择hard negative会导致collapsed models? - 八月的回答 - 知乎
当模型有了坍塌的倾向时，最终loss趋近于margin，近乎于停止更新

使用 offline 离线挖掘策略的Triplet loss实现：

代码参考1：Create a Siamese Network with Triplet Loss in Keras

alpha = 0.2

def triplet_loss(y_true, y_pred):
    anchor, positive, negative = y_pred[:,:emb_size], y_pred[:,emb_size:2*emb_size], y_pred[:,2*emb_size:]
    positive_dist = tf.reduce_mean(tf.square(anchor - positive), axis=1)
    negative_dist = tf.reduce_mean(tf.square(anchor - negative), axis=1)
    return tf.maximum(positive_dist - negative_dist + alpha, 0.)

代码参考2：One Shot learning, Siamese networks and Triplet Loss with Keras

The triplet loss function, implemented as a custom Keras layer

class TripletLossLayer(Layer):
    def __init__(self, alpha, **kwargs):
        self.alpha = alpha
        super(TripletLossLayer, self).__init__(**kwargs)

    def triplet_loss(self, inputs):
        a, p, n = inputs
        p_dist = K.sqrt(K.sum(K.square(a - p), axis=-1))
        n_dist = K.sqrt(K.sum(K.square(a - n), axis=-1))
        return K.mean(K.maximum(p_dist - n_dist + self.alpha, 0), axis=0) + 1e-9

    def call(self, inputs):
        loss = self.triplet_loss(inputs)
        self.add_loss(loss)
        return loss

margin=0.2
loss_layer = TripletLossLayer(alpha=margin)([encoded_a,encoded_p,encoded_n])
network_train = Model(inputs=[anchor_input,positive_input,negative_input],outputs=loss_layer)

代码参考3：tensorflow-addons 的Triplet loss实现

import tensorflow_addons as tfa

model.compile(optimizer='adam',
              loss=tfa.losses.TripletSemiHardLoss(),
              metrics=['accuracy'])import tensorflow_addons as tfa

tfa.losses.metric_learning.triplet_semihard_loss(
    labels, embeddings, margin=1.0
)

使用online挖掘的策略的Triplet loss实现：

https://github.com/eroj333/learning-cv-ml/blob/master/SNN/Online Triplet Mining.ipynb
PyTorch已经集成进去了TripletMarginLoss

Lifted Structured Loss

Lifted Structured Loss (Song et al. 2015) 利用一个训练批次中的所有成对边来提高计算效率。

N-Pairs Loss

Improved Deep Metric Learning with Multi-class N-pair Loss Objective

contrastive loss和triplet loss存在着比如收敛慢，陷入局部最小值等问题，相当部分原因就是因为loss function仅仅只使用了一个negative样本，在每次更新时，与其他的negative的类没有交互。因此，Multi-Class N-pair loss (Sohn 2016) 提出了一个考虑多个negative样本的方法：即从（N-1）个negative样本中区分一个positive样本，当N=2时，即是triplet loss。训练样本为 $\left\{x, x^{+}, x_{1}, \cdots, x_{N-1}\right\}$： $x^{+}$ 是一个positive样本， $\left\{x_{i}\right\}_{i=1}^{N-1}$ 是（N-1）个negative 样本。

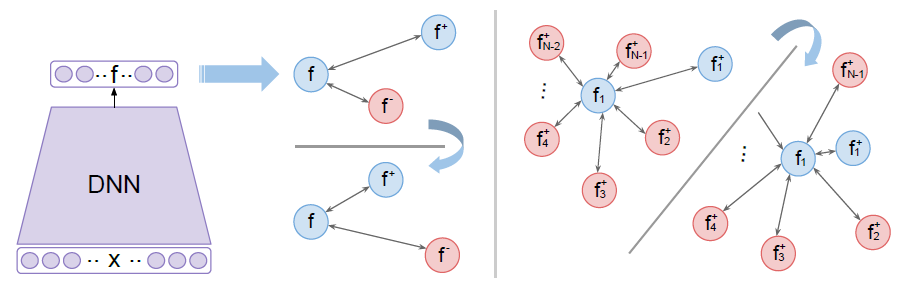
Triplet loss在将positive样本拉近的同时一次只能推离一个negative样本；而(N+1)-tuplet loss基于样本之间的相似性，一次可以将（N-1）个negative样本推离。另外，对比损失和三元组损失都利用欧氏距离来量化点之间的相似性。而 N-Pairs损失利用余弦相似度来量化点之间的相似度，由于余弦相似度度量（以及概率）是尺度不变的（如下图所示），N-pair loss 往往对训练过程中的特征变化具有鲁棒性。Multi-Class N-pair loss 公式如下：

$\begin{aligned}
\mathcal{L}_{\mathrm{tri}}^{m}\left(x, x^{+}, x^{-} ; f\right)&=\max \left(0,\left|f-f^{+}\right|_{2}^{2}-\left|f-f^{-}\right|_{2}^{2}+m\right) \\
&→Euclidean Distance→Cosine Similar,m=0 \\
&=\max (0,f^T f_i-f^T f^{+}) \\
&→softplus(x)=log(1+e^x)≈max(0,x) \\
&=log (1+exp(f^T f_i-f^T f^{+})) \\
\end{aligned}$

扩展到(N-1)个negative样本：

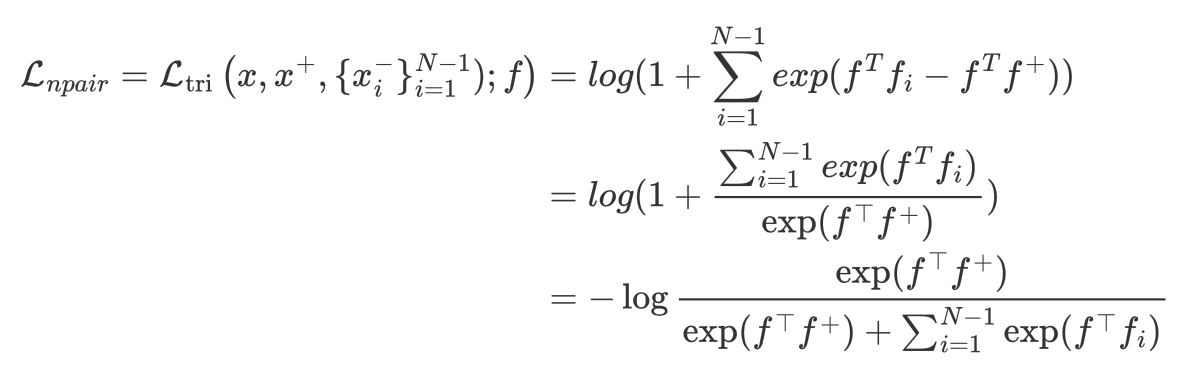
N-pairs的直觉是利用batch中的所有负样本来指导梯度更新，从而加速收敛。N-pairs损失通常优于三元组损失，而且没什么要注意的东西。训练batch的大小的上限是由训练类的数量决定的，因为每个类只允许有一个正样本对。相比之下，三元组损失和对比损失batch的大小仅受GPU内存的限制。此外，N-pairs损失学习了一个没有归一化的嵌入。这有两个结果：(1)不同类之间的边界是用角度来定义的，(2)可以避免退化的嵌入增长到无限大，一个正则化器，来约束嵌入空间，是必需的。

代码参考：

import tensorflow_addons as tfa

tf.contrib.losses.metric_learning.npairs_loss(
    labels, embeddings_anchor, embeddings_positive, reg_lambda=0.002,
    print_losses=False
)

Constellation Loss

论文题目：Constellation Loss: Improving the efficiency of deep metric learning loss functions for optimal embedding
Source code is available at: https://git.code.tecnalia.com/comvis_public/piccolo/ constellation_loss/

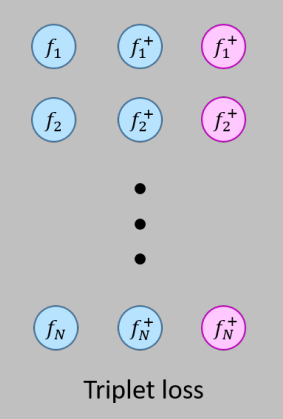
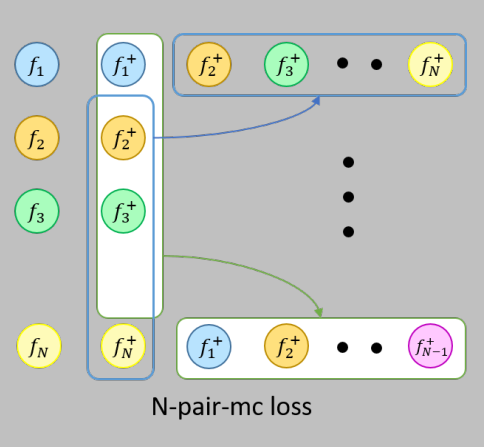
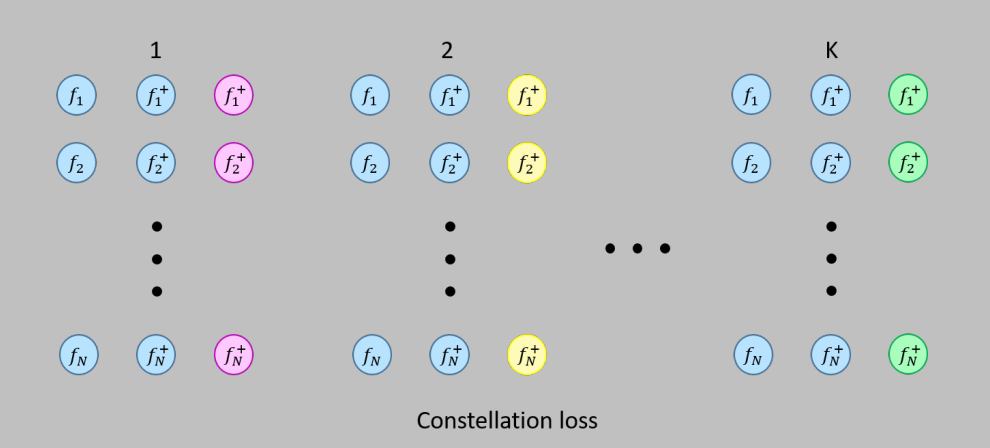
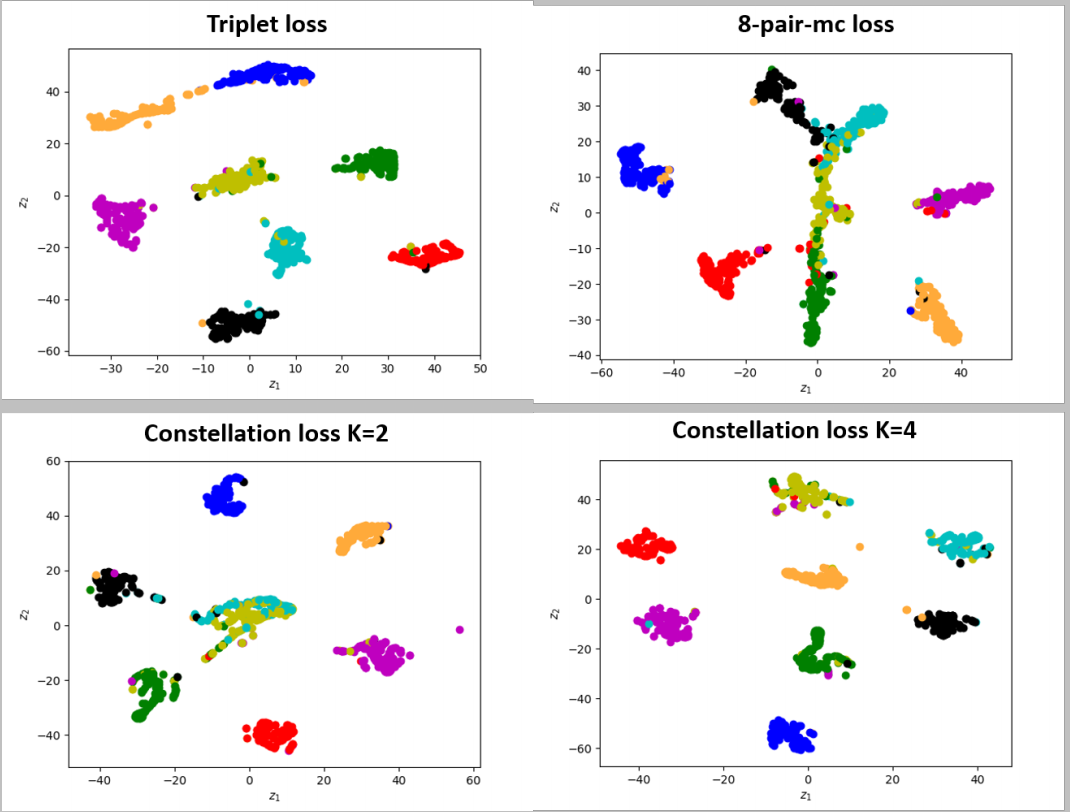
论文主要贡献：把Triplet loss和Multiclass-N-pair loss的函数结合起来，构造了一个新的损失函数，在一个大肠癌组织切片的数据集上获得了比Triplet loss和Multiclass-N-pair loss更好的分类效果。

Triplet loss的损失函数：$\mathcal{L}_{\text {triplet}}=\frac{1}{N} \sum_{i=1}^{N} \max \left(0,\left|f_{i}^{a}-f_{i}^{p}\right|_{2}^{2}-\left|f_{i}^{a}-f_{i}^{n}\right|_{2}^{2}+\alpha\right)$

Multiclass-N-pair loss损失函数：$\mathcal{L}_{m-c}=\frac{1}{N} \sum_{i=1}^{N} \log \left(1+\sum_{j \neq i} \exp \left(f_{i}^{\top} f_{j}^{+}-f_{i}^{\top} f_{i}^{+}\right)\right)$

Constellation Loss损失函数为：$\mathcal{L}_{\text {constellation}}=\frac{1}{N} \sum_{i=1}^{N} \log \left(1+\sum_{j}^{K} \exp \left(f_{i}^{a \top} f_{j}^{n}-f_{i}^{a \top} f_{i}^{p}\right)\right)$

可以看到论文提出的损失函数可以获得更好的聚类效果：

NCE

Noise Contrastive Estimation 前世今生——从 NCE 到 InfoNCE（一堆公式推导….）
Noise Constractive Estimation 噪声对比估计—知乎
 On word embeddings - Part 2: Approximating the Softmax - Ruder
知乎麋路的回答 - 求通俗易懂解释下nce loss？
“噪声对比估计”杂谈：曲径通幽之妙—苏剑林

NCE，也就是 Noise Contrastive Estimation（噪声对比估计），由Gutmann & Hyvarinen在 2010 年提出，将概率估计问题转化为二分类问题，用二分类的最大似然估计替代原始问题。

NCE 的核心思想就是通过学习数据分布样本和噪声分布样本之间的区别，从而发现数据中的一些特性，因为这个方法需要依靠与噪声数据进行对比，所以称为“噪声对比估计（Noise Contrastive Estimation）”。更具体来说，NCE 通过逻辑回归将问题转换成了一个二分类问题，分类器能够对数据样本和噪声样本进行二分类，利用已知的噪声概率分布，来估计未知的经验概率分布。

（以下内容主要参考：https://mp.weixin.qq.com/s/QlrxIZ8wNjmcFVoB78l9ag）

以语言模型举例。现在假设一个特定上下文$c$的数据分布为$\hat{p}(w|c)$—未知，我们称从它里面取出的样本为正样本，令类别$D=1$; 而另一个与$c$无关的噪声分布为$q(w)$, 我们称从里面取出的样本为负样本,令类别为$D=0$。遵循 Gutmann and Hyvrinen (2012) 中的设置, 假设现在取出了$k_d$个正样本和$k_n$个负样本, 将这些正负样本混合形成一个混合分布$p(w|c)$。

我们得到下面这些概率:

所以可以计算后验概率:

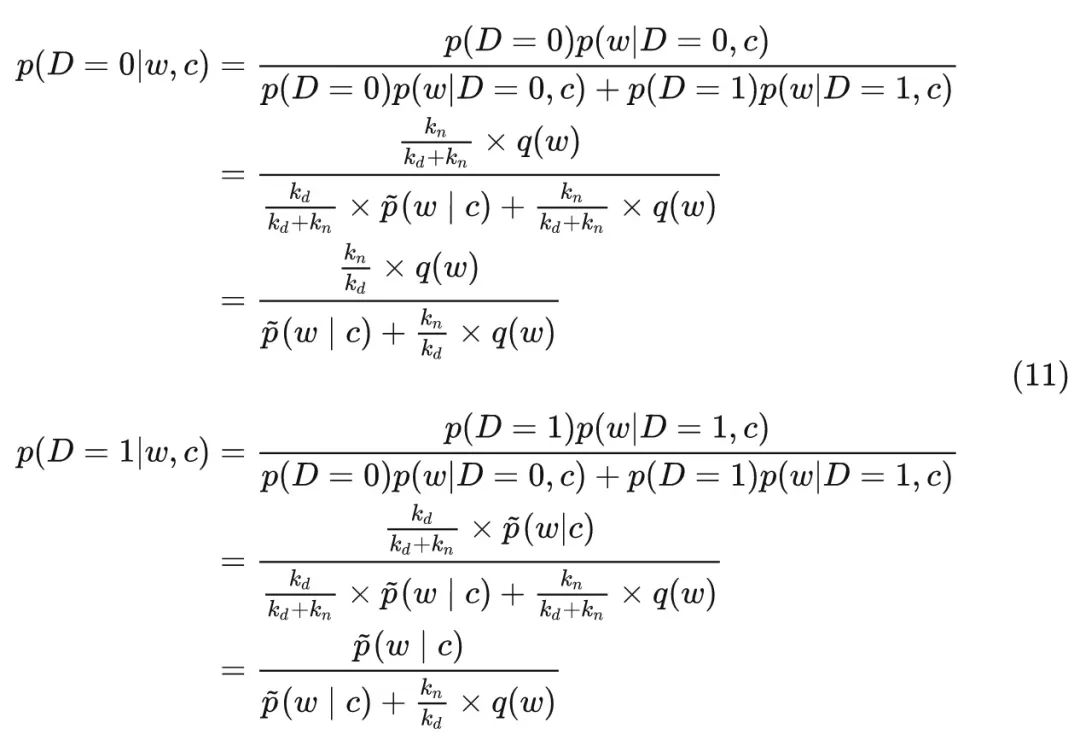
我们令负样本和正样本的比例为$k=\frac{k_n}{k_d}$，则有：

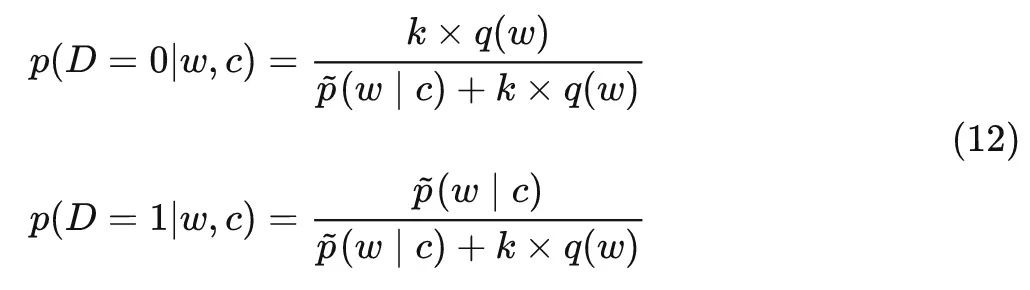
现在我们观察 (12) 式, NCE 所做的事情就是将式中的经验分布$\hat{p}(w|c)$替换成概率模型$p_\theta(w|c)$, 使后验概率成为参数为$\theta$的函数。……我们直接令$p_\theta(w|c)=u_\theta(w|c)$，那么 (12) 式可以写成如下形式：

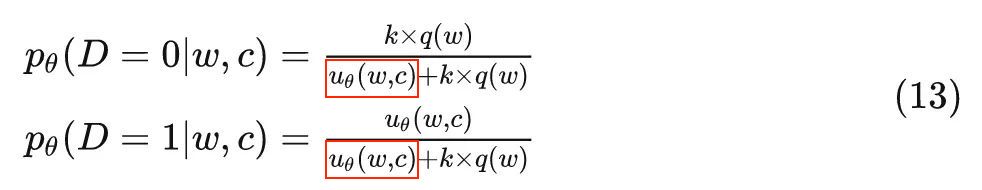
现在我们有了参数为$\theta$的二元分类问题, 假设标签$D_t$为伯努利分布, 那么很容易写出他的条件对数似然$L_{NCE}^c$如下, 实际上在它前面加上负号后, $-L_{NCE}^c$也就等价于 logistics 分类里的 log loss，或者说交叉嫡损失函数：

而 NCE 的目标函数还需要在 (14) 式的基础上除以正样本的数量$k_d$，即

当数据数量很大时，根据大数定律，上式也可以写成：

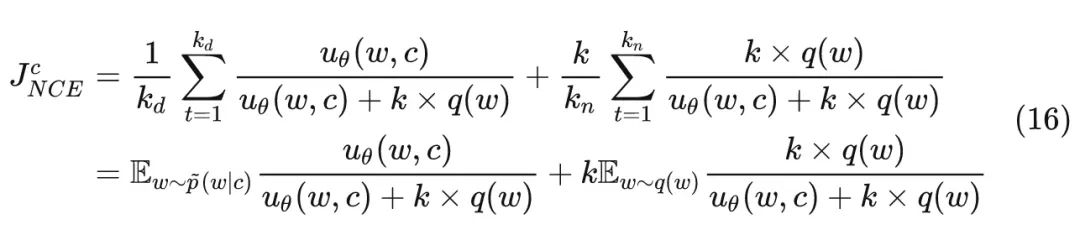
要最大化上述对数似然函数，也就是最大化如下目标函数：

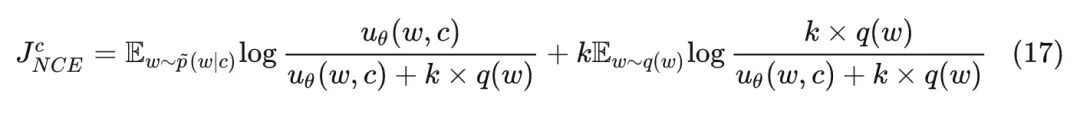
通过 NCE 转换后的优化目标，本质上就是对极大似然估计方法的一种近似，并且随着负样本和正样本数量比$k$的增大，这种近似越精确，这也解释了为什么作者建议我们将$k$设置的越大越好。

InfoNCE

对比学习损失（InfoNCE loss）与交叉熵损失的联系，以及温度系数的作用

InfoNCE 也被称为 NTXentLoss，是 NPairs Loss 的一般形式，被广泛用于自监督学习中。IInfoNCE 继承了 NCE 的基本思想，升级为使用分类交叉熵损失来识别一组不相关的噪声样本中的正样本，并且证明了减小这个损失函数相当于增大互信息 (mutual information) 的下界，这也是名字infoNCE的由来。具体细节这里不再赘述，感兴趣的读者可以参考这篇文章：http://karlstratos.com/notes/nce.pdf，里面有比较清晰的介绍与推导。

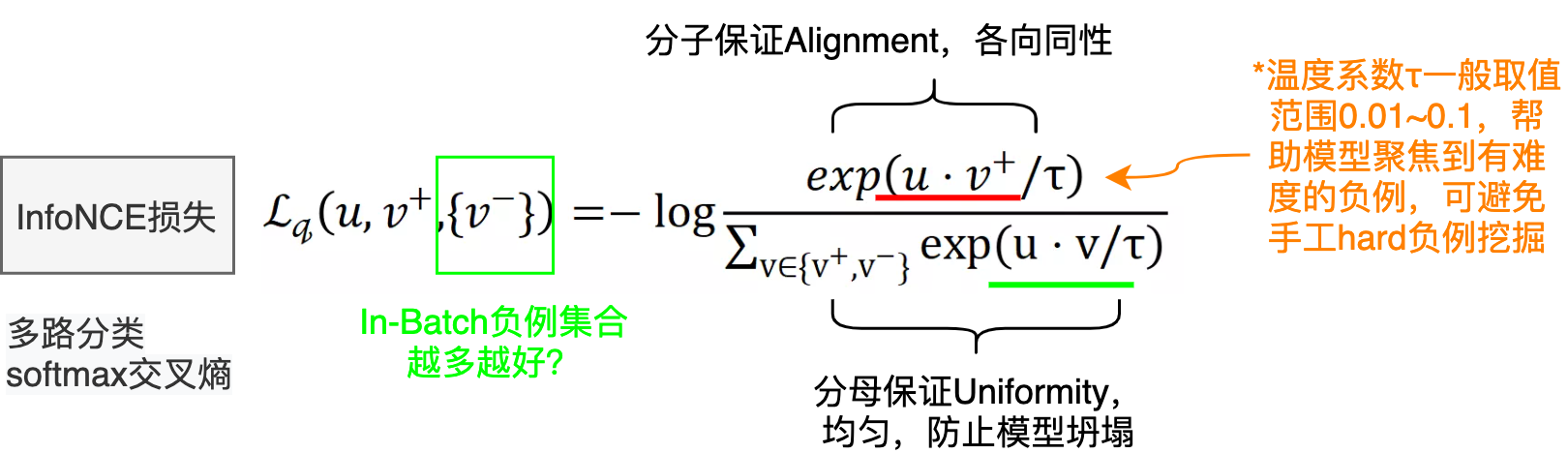
其中 $u$、$v^+$、$u^-$ 分别为原样例、正样例、负样例归一化后的表示，$t$ 为温度超参。

显而易见，infoNCE最后的形式就是多元分类任务常见的交叉熵损失（Cross Entropy Loss for N-way softmax classifier)，使用分类交叉熵损失在一组负样本中识别正样本。因为表示已经归一化，据前所述，向量内积等价于向量间的距离度量。故由softmax的性质，上述损失就可以理解为，我们希望在拉近原样例与正样例距离的同时，拉远其与负样例间的距离，这正是对比学习的思想。

1、InfoNCE和交叉熵损失的关系？

我们先从softmax说起，下面是softmax公式：

交叉熵损失函数如下：

在有监督学习下，ground truth是一个one-hot向量，softmax的结果$\hat{y}_+$取$-log$，再与ground truth相乘之后，即得到如下交叉熵损失：

上式中的 k 在有监督学习里指的是这个数据集一共有多少类别，比如CV的ImageNet数据集有1000类，k就是1000。

对于对比学习来说，理论上也是可以用上式去计算loss，但是实际上是行不通的。为什么呢？

还是拿ImageNet数据集来举例，该数据集一共有128万张图片，我们使用数据增强手段（例如，随机裁剪、随机颜色失真、随机高斯模糊）来产生对比学习正样本对，每张图片就是单独一类，那k就是128万类，而不是1000类了，有多少张图就有多少类。但是softmax操作在如此多类别上进行计算是非常耗时的，再加上有指数运算的操作，当向量的维度是几百万的时候，计算复杂度是相当高的。所以对比学习用上式去计算loss是行不通的。

怎么办呢？NCE loss可以解决这个问题。

NCE（noise contrastive estimation）核心思想是将多分类问题转化成二分类问题，一个类是数据类别 data sample，另一个类是噪声类别 noisy sample，通过学习数据样本和噪声样本之间的区别，将数据样本去和噪声样本做对比，也就是“噪声对比（noise contrastive）”，从而发现数据中的一些特性。但是，如果把整个数据集剩下的数据都当作负样本（即噪声样本），虽然解决了类别多的问题，计算复杂度还是没有降下来，解决办法就是做负样本采样来计算loss，这就是estimation的含义，也就是说它只是估计和近似。一般来说，负样本选取的越多，就越接近整个数据集，效果自然会更好。

有了NCE loss，为什么还要用Info NCE loss呢？

Info NCE loss是NCE的一个简单变体，它认为如果你只把问题看作是一个二分类，只有数据样本和噪声样本的话，可能对模型学习不友好，因为很多噪声样本可能本就不是一个类，因此还是把它看成一个多分类问题比较合理（但这里的多分类 k 指代的是负采样之后负样本的数量，下面会解释）。于是就有了InfoNCE loss，公式如下：

上式中，$q·k$是模型出来的logits，相当于上文softmax公式中的$z$，$τ$是一个温度超参数，是个标量，假设我们忽略$τ$，那么infoNCE loss其实就是cross entropy loss。唯一的区别是，在cross entropy loss里，k指代的是数据集里类别的数量，而在对比学习InfoNCE loss里，这个k指的是负样本的数量。上式分母中的sum是在1个正样本和k个负样本上做的，从0到k，所以共k+1个样本，也就是字典里所有的key。恺明大佬在MoCo里提到，InfoNCE loss其实就是一个cross entropy loss，做的是一个k+1类的分类任务，目的就是想把 q 这个图片分到$k_+$这个类。

另外，我们看下图中MoCo的伪代码，MoCo这个loss的实现就是基于cross entropy loss。

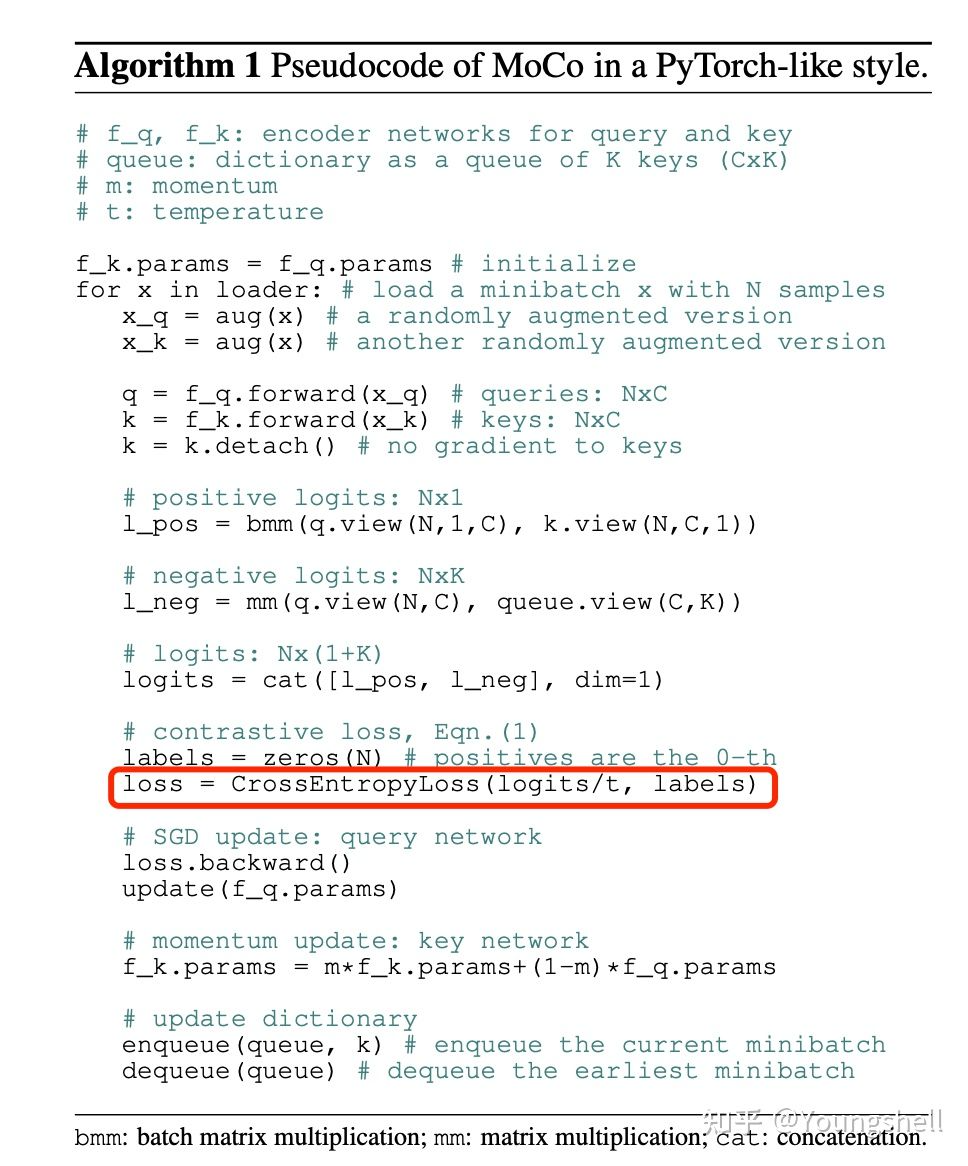
2、温度系数的作用

温度系数$τ$虽然只是一个超参数，但它的设置是非常讲究的，直接影响了模型的效果。上式Info NCE loss中的$q·k$相当于是logits，温度系数可以用来控制logits的分布形状。对于既定的logits分布的形状，当$τ$值变大，则$1 / τ$就变小，$q·k / τ$则会使得原来logits分布里的数值都变小，且经过指数运算之后，就变得更小了，导致原来的logits分布变得更平滑。相反，如果$τ$取得值小，$1 / τ$就变大，原来的logits分布里的数值就相应的变大，经过指数运算之后，就变得更大，使得这个分布变得更集中，更peak。

如果温度系数设的越大，logits分布变得越平滑，那么对比损失会对所有的负样本一视同仁，导致模型学习没有轻重。如果温度系数设的过小，则模型会越关注特别困难的负样本，但其实那些负样本很可能是潜在的正样本，这样会导致模型很难收敛或者泛化能力差。

总之，温度系数的作用就是它控制了模型对负样本的区分度。

Decoupled Contrastive Learning

Decoupled Contrastive Learning (Yann LeCun 2021) 通过分析对比学习中广泛采用的InfoNCE损失，在梯度中确定了一个负-正耦合(NPC)乘数qB，该系数导致模型训练的梯度产生了放缩，使得目前的自监督方法严重依赖于大 Batch Size

由此修改了InfoNCE的公式消除qB的影响，去除分母中的正例对，得到解耦对比学习损失：

$\begin{aligned}
\mathcal{L}_{\text {DC }}&=\mathbb{E}[\mathcal{L}_{DC,i}] \\
\mathcal{L}_{DC,i}&=-\log \frac{ f(\mathbf{x}, \mathbf{c})}{\cancel{ {f(\mathbf{x}, \mathbf{c})}} + \sum_{\mathbf{x}^{\prime} \in X,x≠x^{\prime}} f\left(\mathbf{x}^{\prime}, \mathbf{c}\right)} \\
&=-\log f(\mathbf{x}, \mathbf{c})+\log \sum_{\mathbf{x}^{\prime} \in X,x≠x^{\prime}} f\left(\mathbf{x}^{\prime}, \mathbf{c}\right) \\
\mathcal{L}_{DC,i}^{(k)}&=-\log \frac{\exp \left(\left\langle\mathbf{z}_{i}^{(1)}, \mathbf{z}_{i}^{(2)}\right\rangle / \tau\right)}{\cancel{\exp \left(\left\langle\mathbf{z}_{i}^{(1)}, \mathbf{z}_{i}^{(2)}\right\rangle / \tau\right)}+\sum_{l \in\{1,2\}, j \in[1, N], j \neq i} \exp \left(\left\langle\mathbf{z}_{i}^{(k)}, \mathbf{z}_{j}^{(l)}\right\rangle / \tau\right)} \\
&=-\left\langle\mathbf{z}_{i}^{(1)}, \mathbf{z}_{i}^{(2)}\right\rangle / \tau+\log \sum_{l \in\{1,2\}, j \in[1, N], j \neq i} \exp \left(\left\langle\mathbf{z}_{i}^{(k)}, \mathbf{z}_{j}^{(l)}\right\rangle / \tau\right)
\end{aligned}$

Angular Loss √

Angular loss解决了三元组损失的两个限制。首先，三元组损失假设在不同类别之间有固定的margin _m_。固定的margin是不可取的，因为不同的类有不同的类内变化，如下图所示：

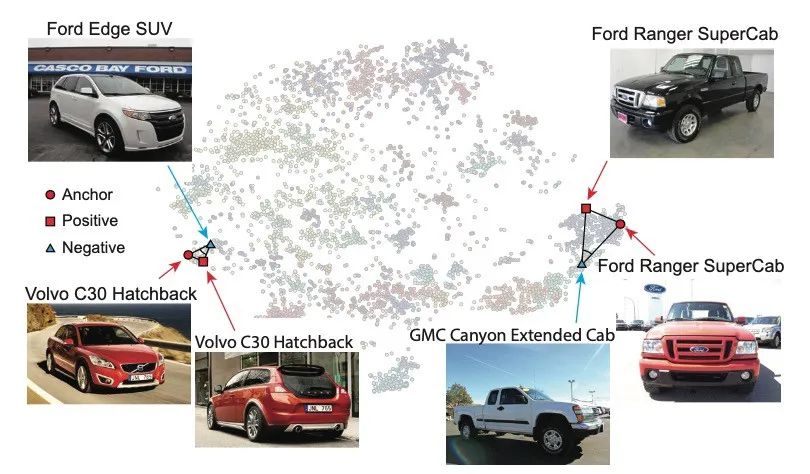
第二个限制是三元组损失是如何产生负样本的梯度的。下图显示了为什么负梯度的方向可能不是最佳的，也就是说，不能保证远离正样本的类中心。

为了解决这两个限制，作者建议使用n的角度代替margin m，并在负样本点$x_n$处纠正梯度。不是基于距离把点往远处推，目标是最小化角度n，即，使三角形a-n-b在n点处的角度更小。下一个图说明angular loss的公式将负样本点$x_n$推离$x_c$，$x_c$为由$x_a$和$x_p$定义的局部簇的中心。另外，锚点$x_a$和正样本点$x_p$被彼此拖向对方。

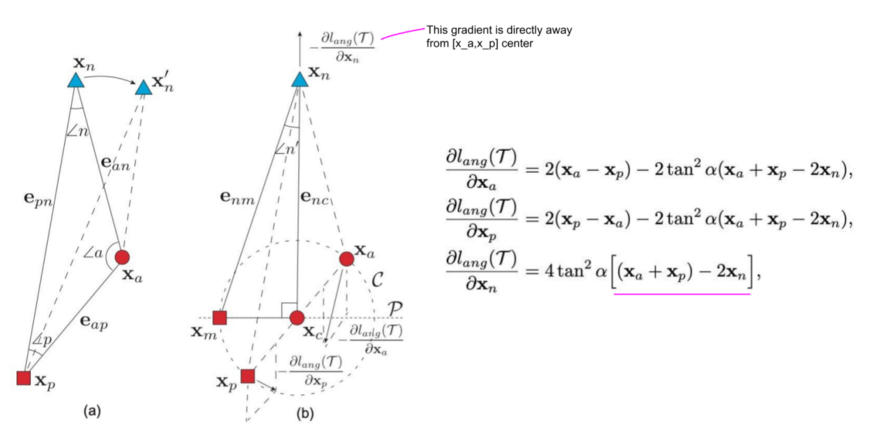
与原来的三元组损耗只依赖于两点(例如 $grad = x_a - x_n$)相比，angular loss的梯度要稳健得多，因为它们同时考虑了所有三点。另外，请注意，与基于距离的度量相比，操纵角度$n ‘$不仅是旋转不变的，而且本质上也是尺度不变的。我的一些建议: N-pairs和Angular loss通常优于原始的三元组损失。然而，在比较这些方法时，需要考虑一些重要的参数。

用于训练三元组损失的采样策略会导致显著的性能差异。如果避免了模型崩溃，困难样本挖掘是有效的，并且收敛速度更快。
训练数据集的性质是另一个重要因素。当进行行人重识别或人脸聚类时，我们可以假设每个类由单个簇表示，即具有小的类内变化的单一模式。然而，一些检索数据集，如CUB-200-2011和Stanford Online Products有很多类内变化。根据经验，hard triplet loss在人/人脸再识别任务中工作得更好，而N-pairs和 Angular losses在CUB-200和Stanford Online Product数据集上工作得更好。
当使用一个新的检索任务和调整一个新的训练数据集的超参数(学习率和batch_size)时，我发现semi-hard三元组损失是最稳定的。它没有达到最好的性能，但它是最不可能退化的。

SupConLoss

Supervised Contrastive Learning.
https://zhuanlan.zhihu.com/p/143443691

文章借鉴并改进self-supervised learning的方法来解supervised 的问题。相较于传统的cross entropy损失函数提升了一个点。并且模型更加robustness和stable。
文章主要的创新点在于利用已有的label信息来将自监督的损失函数（如公式1所示）改造成支持multiple positives 和 multiple negatives（如公式2所示）。

作者通过梯度计算的角度说明了文中提出的loss可以更好地关注于 hard positives and negatives，从而获得更好的效果。

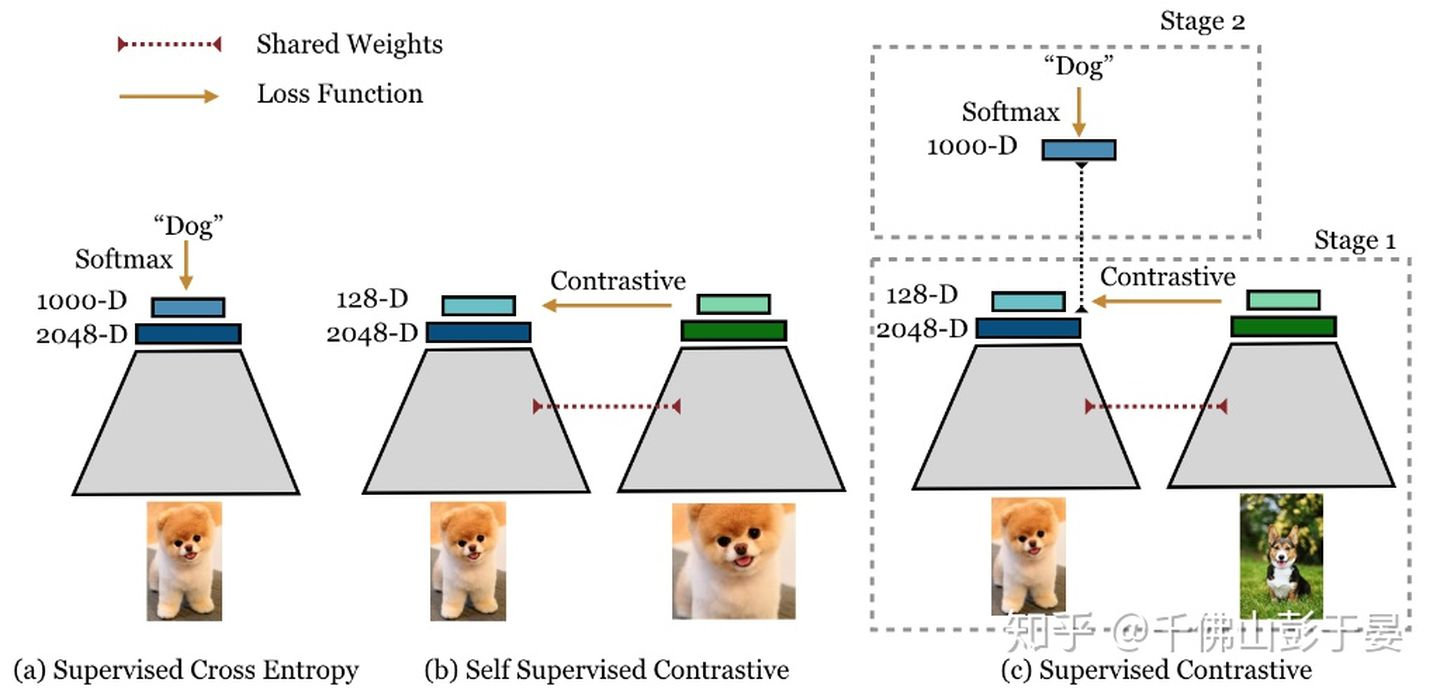
Figure 1: Cross entropy, self-supervised contrastive loss and supervised contrastive loss.

如图1所示，对每一幅图像使用两种随机的不同的augmentations，这样就有了2N幅图像作为一个batch。Supervised Contrastive的训练过程包括以下两步：
- 首先，随机sample训练样本，使用文中提出的Supervised Contrastive Learning训练；
- 第二步，固定representation部分的参数，使用cross-entropy训练分类器部分。（如果只需要获取embedding，不需要做分类的话，不需要执行这一步。）

Classification-based Loss

将距离度量问题作为分类问题和验证问题——> softmax及其变种损失函数Margin-based Softmax

上一部分介绍了metric learning loss function中的 Contrastive loss。除此之外，还有以softmax多分类为代表的一系列classification-based loss。

softmax 主要有两个缺点：

第一点是softmax函数在训练过程中无法同时做到类内相近，类间分离这一目标；
第二点是数据不平衡问题。

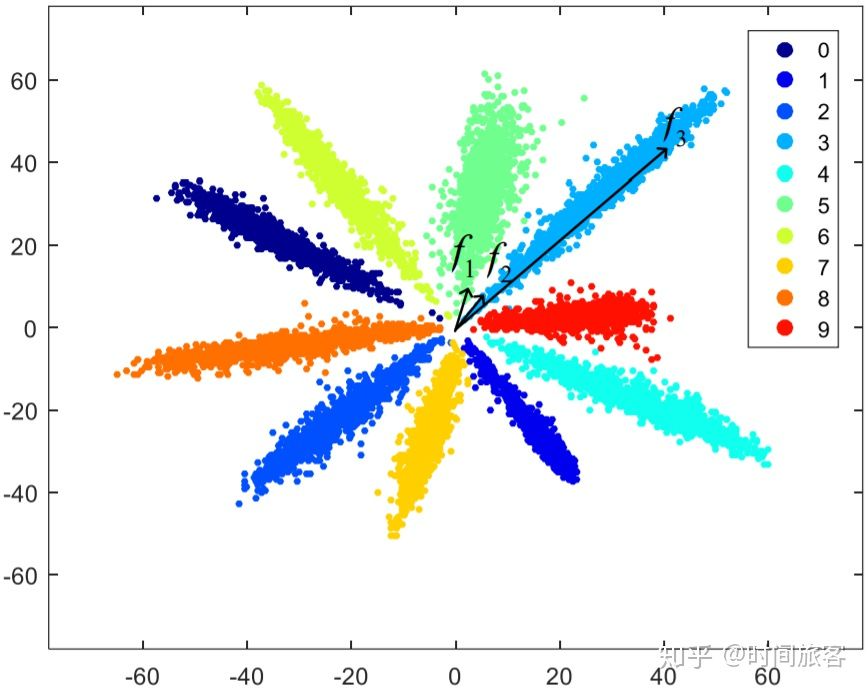
softmax函数没有类内相近，类间分离的约束条件

近年来，面部识别领域的主要技术进展集中在如何改进softmax的损失，使得既能充分利用其易于优化，收敛快的优良性质，又使得其能优化出一个具有优良泛化性的度空间。而这些技术改进主要又能被归为两大类别：

引入 margin，达到了类间分离的目的，使得 Softmax Loss 能学习到更具有区分性的 metric 空间。
归一化（Normalization）。一个类别具有的样本数越大，相关的权重范数往往越大，通过归一化能够减少长尾数据造成的类间不平衡问题（目前主流的方法中，归一化+伸缩系数s基本成为标配）

先总结几个重要的点：

L-Softmax	首次提出angular margin的概念，重新思考$w*x$，引入cos角，认为各类之间的夹角需要有个margin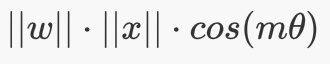
A-Softmax	将weight归一化，使得特征上的点映射到单位超球面上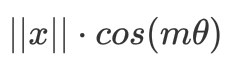
AM-Softmax	将角度上的乘性关系改为cos值的加性关系+特征/权重归一化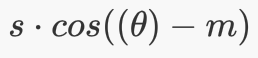
CosFace	同AM-Softmax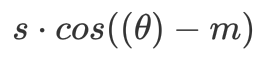
Arcface	将margin由cos外移到内

Normalized Softmax Loss

Classification is a Strong Baseline for Deep Metric Learning

softmax可以起到放大 $x$ 的作用，使模型训练和收敛更容易。例如 x = [4,6]，如果直接算概率，p = [0.4,0.6]；如果用softmax公式计算，p = [0.12, 0.88]。通过softmax的放大，模型不需要把类别概率分的很开就可以得到比较小的loss，这样有利于模型收敛。Normalized Softmax Loss 公式如下：

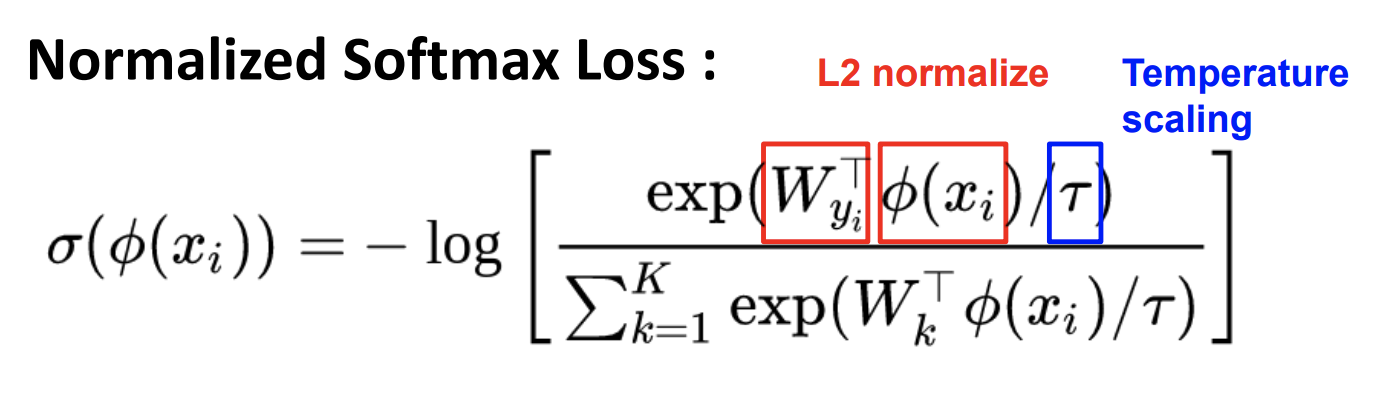
Regularize embedding space to hyphersphere (通过正则化，嵌入超平面/球面)
Temperature scaling to enforce compact intra-class clusters (加入温度超参缩放，使得类内紧凑)

L-Softmax Loss

Large-Margin Softmax Loss for Convolutional Neural Networks

2016年ICML的一篇论文 L-Softmax Loss 首次在softmax上引入了 margin 的概念，具有非常重大的意义。下面给出 L-softmax loss的定义：

$L_{i}=-\log \left(\frac{e^{\left|\boldsymbol{W}_{y_{i}}\right|\left|\boldsymbol{x}_{i}\right| \psi\left(\theta_{y_{i}}\right)}}{e^{\left|\boldsymbol{W}_{y_{i}}\right|\left|\boldsymbol{x}_{i}\right| \psi\left(\theta_{y_{i}}\right)}+\sum_{j \neq y_{i}} e^{\left|\boldsymbol{W}_{j}\right|\left|\boldsymbol{x}_{i}\right| \cos \left(\theta_{j}\right)}}\right)$

where

$\begin{array}{c}
\psi(\theta)=\left\{\begin{array}{cc}
\cos (m \theta), & 0 \leq \theta \leq \frac{\pi}{m} \\
D(\theta), & \frac{\pi}{m}<\theta \leq \pi
\end{array}\right.
\end{array}$

其中 m 是整数，它决定类内的聚拢程度，能够使对应类别的夹角扩大m倍。m 值越大则分类边缘越大，同时学习目标就越难。那么为什么会有这种效果呢？个人理解，以前分类的类内角度搜索范围是 $θ∈[0,π]$，在加了 m以后，它的范围缩小到 $\frac{\theta}{m} \in\left[0, \frac{\pi}{m}\right]$。因此类内间距就变小了。

对于增加 margin 的形象解释，文章给出了一个很好的示意图（类内距离尽可能小，类间距离尽可能大）。

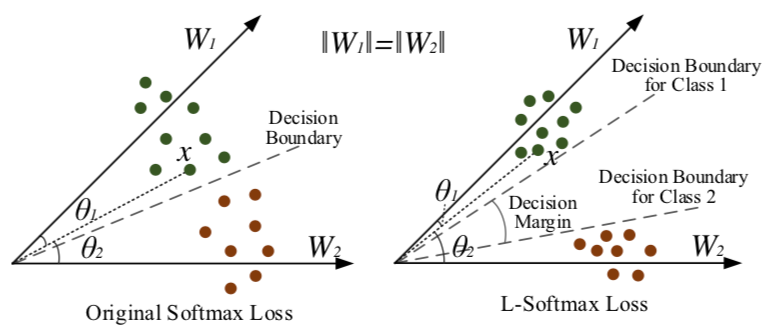
$\theta_{1(2)}$ 表示特征 x 和类权重 $W_{1(2)}$ 的夹角。

先简化问题成一个二元分类的例子，假设类权重被归一化了，此时夹角就决定了样本x被分到哪一类。左边是原始的softmax loss，分界面是在两类别的中间$\theta_{1}=\theta_{2}$ ，此时（训练）样本紧贴着分界面。测试的时候，就容易混淆了。右边是L-Softmax，为了在两类中间留下空白（margin），要求分界面是 $m\theta_{1}=\theta_{2}, m>1$ 。此时为了分类正确，样本特征会被压缩到一个更小的空间，两个类别的分类面也会被拉开。容易看出，此时两个类之间的 angular decision margin 是 $\frac{m-1}{m+1} \theta_{1,2}$，其中 $\theta_{1,2}$ 是类权重$W_1$和$W_2$的夹角。

A-softmax Loss

深度学习—A-softmax原理+代码
 SphereFace: Deep Hypersphere Embedding for Face Recognition

2017 年 CVPR 的 _[SphereFace]_ 在 L-Softmax 的基础上引入了权重归一化 (weight normalization)，对权值 w 进行了单位化，并将 bias 置零，即$||W||=1$ 和 $b=0$，这样判别条件 $\left|w_{1}\right||x| \cos \left(m \theta_{1}\right)>\left|w_{2}\right||x| \cos \left(\theta_{2}\right)$ 仅由角度(angular)距离决定。

为什么要添加 |w|=1 的约束呢？作者做了两方面的解释，一个是softmax loss学习到的特征，本来就依据角度有很强的区分度，另一方面，人脸是一个比较规整的流形，将其特征映射到超平面表面也好解释。

这样便得到了angular softmax loss，简称A-softmax loss。_[SphereFace]_ 提出的 loss 的具体形式是：

$L=\frac{1}{N} \sum_{i}-\log \left(\frac{e^{\left|\mathbf{x}_{i}\right| \cdot \cos \left(m \cdot \theta_{y_{i}, i}\right)}}{e^{\left|\mathbf{x}_{i}\right| \cdot \cos \left(m \cdot \theta_{y_{i}, i}\right)}+\sum_{j \neq y_{i}} e^{\left|\mathbf{x}_{i}\right| \cdot \cos \theta_{j, i}}}\right)$

_[SphereFace]_ 作者通过一个很形象的特征分布图，展示了引入 margin 的效果，可见，随着 margin 的增加，类内被压缩的更紧凑，类间的界限也变得更加清晰了。

此外，在归一化方向，王峰大佬发表的 NormFace 论文提出 L2-softmax，进一步对特征向量做 L2 归一化，即feature normalization，数学上的工作非常漂亮。而且发现了feature normalization后网络难以收敛的问题，提出需要在 _L_2 超球面嵌入后引入尺度因子的办法来解决这一问题。此外，作者还解释了 _L_2 归一化在难例挖掘和处理类不均衡问题上的作用。_L_2 超球面嵌入目前已经成为业内的标准做法。

代码实现：苏剑林 bojone/margin-softmax

def sparse_simpler_asoftmax_loss(y_true, y_pred, scale=30):
    y_true = K.expand_dims(y_true[:, 0], 1) # 保证y_true的shape=(None, 1)
    y_true = K.cast(y_true, 'int32') # 保证y_true的dtype=int32
    batch_idxs = K.arange(0, K.shape(y_true)[0])
    batch_idxs = K.expand_dims(batch_idxs, 1)
    idxs = K.concatenate([batch_idxs, y_true], 1)
    y_true_pred = K.tf.gather_nd(y_pred, idxs) # 目标特征，用tf.gather_nd提取出来
    y_true_pred = K.expand_dims(y_true_pred, 1)
    # 用到了四倍角公式进行展开
    y_true_pred_margin = 1 - 8 * K.square(y_true_pred) + 8 * K.square(K.square(y_true_pred))
    # 下面等效于min(y_true_pred, y_true_pred_margin)
    y_true_pred_margin = y_true_pred_margin - K.relu(y_true_pred_margin - y_true_pred)
    _Z = K.concatenate([y_pred, y_true_pred_margin], 1) # 为计算配分函数
    _Z = _Z * scale # 缩放结果，主要因为pred是cos值，范围[-1, 1]
    logZ = K.logsumexp(_Z, 1, keepdims=True) # 用logsumexp，保证梯度不消失
    logZ = logZ + K.log(1 - K.exp(scale * y_true_pred - logZ)) # 从Z中减去exp(scale * y_true_pred)
    return - y_true_pred_margin * scale + logZ

乘性 margin 的弊端

总之，A-Softmax 对分类权重进行归一化，将偏差归零，并引入可以用参数_m_控制的角边距来学习具有判别性和清晰几何解释的特征。但引入 margin 之后，有一个很大的问题，网络的训练变得非常非常困难。在 _[SphereFace]_ 中提到需要组合退火策略等极其繁琐的训练技巧。这导致这种加 margin 的方式极其不实用。而事实上，这一切的困难，都是因为引入的 margin 是乘性 margin 造成的。我们来分析一下，乘性 margin 到底带来的麻烦是什么：

第一点，乘性 margin 把 cos 函数的单调区间压小了，导致优化困难。对，在处在区间 [0,π] 时，是一个单调函数，也就是说落在这个区间里面的任何一个位置，网络都会朝着把减小的方向优化。但加上乘性 margin m 后的单调区间被压缩到了，那如果恰巧有一个 sample 的落在了这个单调区间外，那网络就很难优化了；
第二点，乘性 margin 所造成的 margin 实际上是不均匀的，依赖于的夹角。前面我们已经分析了，两个 class 之间的 angular decision margin ，其中是两个 class 的 weight 的夹角。这自然带来一个问题，如果这两个 class 本身挨得很近，那么他们的 margin 就小。特别是两个难以区分的 class，可能它们的 weight 挨得特别近，也就是几乎接近 0，那么按照乘性 margin 的方式，计算出的两个类别的间隔也是接近 0 的。换言之，乘性 margin 对易于混淆的 class 不具有可分性。

AM-softmax Loss

论文：Additive Margin Softmax for Face Verification
注：腾讯AI Lab的 CosFace: Large Margin Cosine Loss for Deep Face Recognition和AM-Softmax算法基本一致，工作也几乎是同时完成，两篇论文也都各自中了不同的会议。

为了解决上述提到的两个乘性 margin 的弊端，AM-softmax（additive margin softmax loss）提出了一种加性间隔margin策略，对Softmax损失的目标logit进行特征和权重归一化。

相比于A-softmax只能施加不固定的角间距，它则施加固定的角间距。
将L-softmax和A-softmax中的乘性margin改为加性margin，即 $cos(m\theta)$ 改成 $cos(\theta)-m$，同时加上了尺度因子s，使得前向后向传播变得更加简单，性能也更好。

最后，AM-Softmax 损失可以定义如下。

$L_i=-\log \left(\frac{e^{s \cdot\left(\cos \theta_{t}-m\right)}}{e^{s \cdot\left(\cos \theta_{t}-m\right)}+\sum_{i \neq t} e^{s \cdot \cos \theta_{i}}}\right)$

其中，$θ_i$代表$z,ci$的夹角。

在 AM-Softmax 原论文中，所使用的是 $s=30,m=0.35$。s的存在是必要的，因为cos函数本身是有界的，范围是[−1,1]，如果进行softmax，那么概率其实会很均衡，比如[1, 0, 0, -1]的softmax是[0.53444665, 0.19661193, 0.19661193, 0.07232949]，也就是说目标概率很难达到1，loss就降不下去，所以需要做好比例缩放，才允许pt能足够接近于1（有必要的话）。当然，s并不改变相对大小，因此这不是核心改变，核心是原来应该是$cos⁡θ_t$的地方，换成了$cosθ_t−m$加强了条件，迫使类内差距更小，类间差距更大。决策边界为：

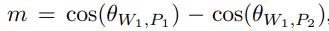
几何解释：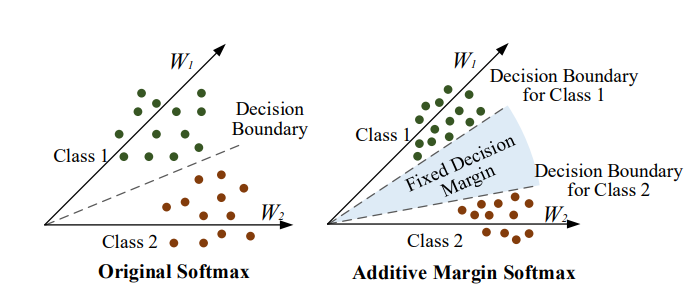

为了更好地可视化 AM-Softmax 损失的效果，使用 7 层 CNN 模型和 Fashion MNIST 数据集将其与其他损失进行了比较。CNN 模型的 3 维特征输出被归一化并绘制在一个超球体（球）中，如下所示。从可视化中，您可以看到 AM-Softmax 在对输出进行聚类时的表现与 SphereFace (A-Softmax) 相似，并且随着边距的增加，m 越大越好。
超球面几何解释[来源]

总之，L-Softmax、A-Softmax 和 AM-Softmax 损失都试图通过在 Softmax 损失中引入一个边距来结合分类和度量学习，旨在最大化类之间的距离并增加相同类之间的紧凑性。在这三者中，AM-Softmax 被证明可以最大程度地提高模型性能，特别是在用于人脸验证的 LFW 和 MegaFace 数据集中。

代码实现：苏剑林 bojone/margin-softmax

def amsoftmax_loss(y_true, y_pred, scale=30, margin=0.35):
    y_pred = y_true * (y_pred - margin) + (1 - y_true) * y_pred
    y_pred *= scale
    return K.categorical_crossentropy(y_true, y_pred, from_logits=True)

Sparse版代码实现：苏剑林 bojone/margin-softmax

def sparse_amsoftmax_loss(y_true, y_pred, scale=30, margin=0.35):
    y_true = K.expand_dims(y_true[:, 0], 1) # 保证y_true的shape=(None, 1)
    y_true = K.cast(y_true, 'int32') # 保证y_true的dtype=int32
    batch_idxs = K.arange(0, K.shape(y_true)[0])
    batch_idxs = K.expand_dims(batch_idxs, 1)
    idxs = K.concatenate([batch_idxs, y_true], 1)
    y_true_pred = K.tf.gather_nd(y_pred, idxs) # 目标特征，用tf.gather_nd提取出来
    y_true_pred = K.expand_dims(y_true_pred, 1)
    y_true_pred_margin = y_true_pred - margin # 减去margin
    _Z = K.concatenate([y_pred, y_true_pred_margin], 1) # 为计算配分函数
    _Z = _Z * scale # 缩放结果，主要因为pred是cos值，范围[-1, 1]
    logZ = K.logsumexp(_Z, 1, keepdims=True) # 用logsumexp，保证梯度不消失
    logZ = logZ + K.log(1 - K.exp(scale * y_true_pred - logZ)) # 从Z中减去exp(scale * y_true_pred)
    return - y_true_pred_margin * scale + logZ

PS：为什么改为加性 margin 依然有效果？（来自我的推导）

AAM-softmax Loss

Additive Angular Margin Loss for Deep Face Recognition

与AM-softmax类似，CVPR 2018 提出的 Arcface 也是加性margin，差别只是 _[ArcFace]_ 的 margin 加在 Cos 算子的里面，而 _[AM-Softmax]_ 的 margin 在加性算子的外面。目前classification loss中结果最好的loss应该就是arcface了。Arcface的公式为：

$L_{3}=-\frac{1}{N} \sum_{i=1}^{N} \log \frac{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}}{e^{s\left(\cos \left(\theta_{y_{i}}+m\right)\right)}+\sum_{j=1, j \neq y_{i}}^{n} e^{s \cos \theta_{j}}}$

式中，s代表比例缩放scale超参数，m代表间隔 margin。

在 _[ArcFace]_ 中，作者对集中加 margin 的方式做了很形象的对比，如下图所示。可以看出，_[ArcFace]_ 提出的 margin 更符合“角度”margin 的概念，而 _[CosFace]_ 或是 _[AM-Softmax]_ 更符合 Cosine margin 的概念。

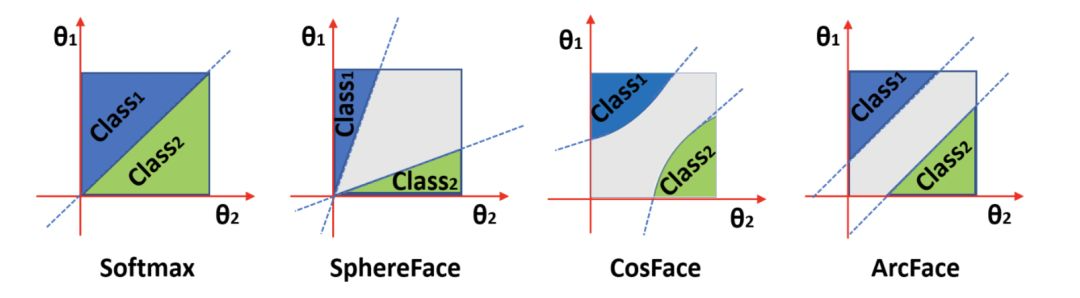
小结

最后，我们总结一下加 margin 的几种 Softmax 的几种形式：

到这里问题还远远没有结束，现存的问题有：

在归一化技巧下，noisy sample 对网络的负面干扰也被放大，如何削弱其影响值得进一步思索；
即使做了 weight 归一化，长尾问题也只是得到一定的缓解，不平衡的问题依然存在；
增加 margin 虽然让网络学到了更好的度量空间，但引入的超参到底怎么样才是最优的选项？

这些问题依然还没有被很好解决。

Circle loss：基于统一视角泛化损失函数

1、CVPR2020的新作circle loss结合使用 softmax loss 和 contrastive loss。
直播回顾 | 旷视 Circle Loss：弥合割裂、统一视角的新型深度特征学习方法
2、作者：biendata https://www.bilibili.com/read/cv7441815 出处：bilibili
3、将“softmax+交叉熵”推广到多标签分类问题

以往metric learning loss的问题

无论是contrast loss和classification loss，它们的核心都是一个目标：类内相近，类间分离。体现到loss function上，就是最大化类内相似度sp，同时最小化类间相似度sn，优化的目标是最小化二者的差值（sn-sp）。然而，这样的优化方式是不够灵活的，每个相似度应当根据其当前优化状态给予不同的优化权重。如果相似性得分偏离最佳值，则应受到严重惩罚。否则，如果相似性分数已接近最佳值，则应进行适度优化。因此，可以把优化目标改进为 $a_ns_n-a_ps_p$ ，其中αn和αp是独立的加权因子，从而允许sn和sp以不同的速度学习。对应到图b，决策边界变成了一个圆形，点A和点B的优化方向都趋近于T，这一改进解决了上述两个问题。

pairwise loss和classification loss的统一形式

对于样本x，假设有K个类内相似度 $s_p^i(i=1,2,…K)$ 以及L个类间相似度 $s_n^j(i=1,2,…L)$，则统一的优化目标为：

其中 $\gamma$ 是伸缩系数，m是margin。这个公式的本质是什么呢？我们需要知晓两个数学上的近似函数，即LogSumExp和Softplus（参考王峰：从最优化的角度看待Softmax损失函数）：

把这三个近似变换公式替换到 L_uni：

经过近似以后，可以看出优化目标是使最小的sp比最大的sn还大margin，和我们期待的优化目标是相符的。而且，L_uni是一个通用loss，可以通过简单变换得到常见的pairwise loss和classification loss，例如AM-softmax loss和triplet loss：

$\begin{aligned}\mathcal{L}_{a m} &=\log \left[1+\sum_{j=1}^{N-1} \exp \left(\gamma\left(s_{n}^{j}+m\right)\right) \exp \left(-\gamma s_{p}\right)\right] \\&=-\log \frac{\exp \left(\gamma\left(s_{p}-m\right)\right)}{\exp \left(\gamma\left(s_{p}-m\right)\right)+\sum_{j=1}^{N-1} \exp \left(\gamma s_{n}^{j}\right)}
\end{aligned}$

circle loss

准备工作已经做完了，我们已经获得了pairwise loss和classification loss的统一形式，也知道了这些loss存在的问题，接下来就在L_uni的基础上进一步改进吧。首先，暂时不考虑margin，并加入自适应的 $a_n$ 和 $a_p$：

假设sp的最优值是Op，sn的最优值为On，并定义：

这个 $a_n$ 和 $a_p$的取值也容易理解：越接近最优值，它的优化力度越小；反之，优化力度越大。接下来，想办法加入刚才忽略的margin。如果模仿之前sn与sp对称时的loss，则只需要把margin加到sn这一项就可以了，但是circle loss中sn和sp不对称，因此需要对sn和sp设置不同的margin：

最后，关于Circle Loss 可以总结为三点：

提出了一个统一的优化视角，来理解主流的损失函数；
Circle Loss使用完全相同的公式，在两种基本学习方式中都获得了极具竞争力的表现。
在一系列常见任务中，Circle Loss取得了稳定的提升。

附录 1：Other names used for Ranking Losses

https://gombru.github.io/2019/04/03/ranking_loss/

Ranking Losses are essentialy the ones explained above, and are used in many different aplications with the same formulation or minor variations. However, different names are used for them, which can be confusing. Here I explain why those names are used.

Ranking loss: This name comes from the information retrieval field, where we want to train models to rank items in an specific order.
Margin Loss: This name comes from the fact that these losses use a margin to compare samples representations distances.
Contrastive Loss: Contrastive refers to the fact that these losses are computed contrasting two or more data points representations. This name is often used for Pairwise Ranking Loss, but I’ve never seen using it in a setup with triplets.
Triplet Loss: Often used as loss name when triplet training pairs are employed.
Hinge loss: Also known as max-margin objective. It’s used for training SVMs for classification. It has a similar formulation in the sense that it optimizes until a margin. That’s why this name is sometimes used for Ranking Losses.

附录 2：Ranking Loss Layers in TF/PyTorch

PyTorch

CosineEmbeddingLoss. It’s a Pairwise Ranking Loss that uses cosine distance as the distance metric. Inputs are the features of the pair elements, the label indicating if it’s a positive or a negative pair, and the margin.
MarginRankingLoss. Similar to the former, but uses euclidian distance.
TripletMarginLoss. A Triplet Ranking Loss using euclidian distance.

TensorFlow