度量学习之 AMSoftmax 理解

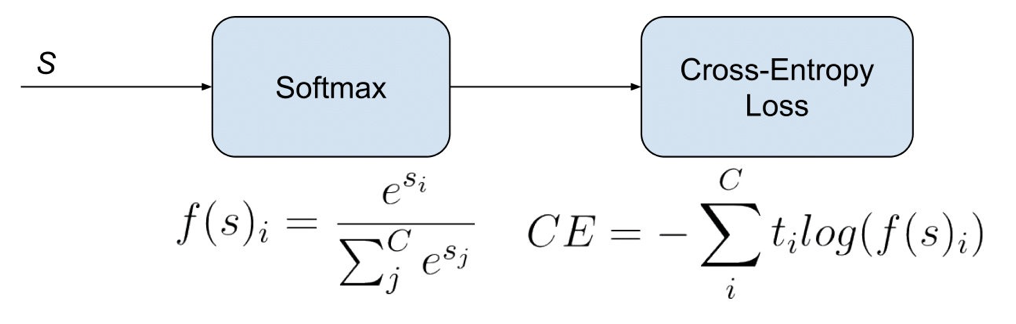
从最优化的角度来推导出Softmax交叉熵损失函数

一般而言，最优化的问题通常需要构造一个目标函数。使用神经网络进行多分类（假设为 $C$ 类)时的目标函数是什么？可以将各个类别的输出独立开来，每个类别占据一个维度。那么如果让一个样本的真值标签（ground-truth label）所对应的分数比其他分数更大，就可以通过比较 $C$ 个分数的大小来判断样本的类别了。

多分类优化目标：

输出C个分数，使目标分数比非目标分数更大。

换成数学描述，设 $z=f(x)∈R^c、y$ 为真值标签的序号，那优化目标即为：

$∀_{j≠y}, z_y>z_j $

利用max函数，让$ z_y $刚刚超过$ z_j $时就停止，防止 z 无限地上升或下降，控制整个神经网络的幅度

$\mathcal{L} =\sum_{i=1,i\neq y}^{C} \max( z_i - z_y, 0)#id=VMd31$

然而这样做往往会使模型的泛化性能比较差，添加一个参数m，让 $z_y$ 比 $z_j$ 大过一定的数值才停止：

$\mathcal{L}_{hinge} = \sum_{i=1,i\neq y}^{C} \max(z_i - z_y + m, 0)#id=ri7LM$

这个 loss 也即hinge loss…

多分类改进的优化目标（大量的非目标分数得到优化，导致的梯度爆炸）：

改进：输出C个分数，使目标分数比最大的非目标分数更大。

这样我们的损失函数就变成了：

$\mathcal{L} = \max( \max_{i\neq y}\{z_i\} - z_y, 0)#id=oTsRi$

问题：每次优化的分数过少，会使得网络收敛极其缓慢，

解决：smooth。

max函数的smooth版是LogSumExp函数：

$\mathcal{L}_{lse} = \max\left( \log\left( \sum_{i=1,i\neq y}^{C}{e^{z_i}} \right) - z_y, 0\right)#id=BqApN$

LogSumExp函数的导数恰好为softmax函数：

$\frac{\partial \log\left( \sum_{i=1,i\neq y}^{C}{e^{z_i}} \right)}{\partial z_j} = \frac{e^{z_j}}{\sum_{i=1,i\neq y}^c{e^{z_i}}}#id=LytbJ$

LogSumExp函数值是大于等于max函数值的，而且等于取到的条件也是非常苛刻的，所以使用LogSumExp函数相当于变相地加了一定的 $m$。

继续smooth：

$\begin{aligned} \mathcal{L}_{softmax} &= \log\left(1 + e^{\log\left( \sum_{i=1,i\neq y}^{C}{e^{z_i}} \right) - z_y}\right)\\ &= \log\left(1 + \frac{\sum_{i=1,i\neq y}^{C}{e^{z_i}}}{e^{z_y}}\right)\\ &= \log\frac{\sum_{i=1}^{C}{e^{z_i}}}{e^{z_y}}\\ &= -\log\frac{e^{z_y}}{\sum_{i=1}^{C}{e^{z_i}}} \end{aligned}#id=rmp2h$

在经过两步smooth化之后，我们将一个难以收敛的函数逐步改造成了大家所熟知的softmax交叉熵损失函数。从这个推导过程中我们可以看出smooth化不仅可以让优化更畅通，而且还变相地在类间引入了一定的间隔，从而提升了泛化性能。

Softmax理解之二分类与多分类

总结一下，Softmax交叉熵损失函数在进行多分类时可以理解为是在训练多个二分类器的组合，只不过因为Softmax训练的是类别向量而不是分界面，所以其训练效率得到了很大的提升。Softmax交叉熵损失函数的多条优良的性质以及它在多个二分类器之间的权重分配方式有助于我们设计其他的损失函数，同时也能启发一下多个损失函数之间加权方式的研究，毕竟Softmax看似是多分类，实际上是有着巧妙设计的权重的多个二分类器，那么其他的多损失函数说不定也能利用一下类似的权重分配方式呢？

Softmax理解之Smooth程度控制

总结一下，softmax 函数中的 $z$ 幅度既不能过大、也不能过小，过小会导致近对目标函数近似效果不佳的问题；过大则会使类间的间隔趋近于0，影响泛化性能。

那么如何去控制 $z$ 的幅度呢？那就是 Softmax 交叉熵损失的温度项 $T$ ：

$\begin{aligned}
\mathcal{L}_{softmax}&=-\log \left(\frac{e^{z_{y}}}{\sum_{i=1}^{C} e^{z_{i}}}\right) \\
&=-\log \left(\frac{e^{\frac{z_{y}}{T}}}{\sum_{i=1}^{C} e^{\frac{z_{i}}{T}}}\right) \\
\end{aligned}$

温度项控制着 Softmax 的 smooth 程度， $T$ 越小，则 Softmax 越接近one-hot max， $T$ 越大，则近似效果越差。注意这个 $T$ 是施加在所有的分数 $z$ 上的，所以这是对分数的一个线性变换，如何让温度项能够生效呢？

答案是将特征和权重全部归一化，这样 $z$ 就从特征与权重的内积变成了特征与权重的余弦，由于余弦值的范围是 $[-1,1]$ ，所以 $z$ 的幅度就大致被定下来了，然后我们再乘上一个尺度因子 $s$ 来拉长 $z$ 的幅度，来保证输入到 Softmax 里的分数能在一个合适的范围：

$\mathcal{L} = -\log\left( {\frac{e^{s\tilde{z_y}}}{\sum_{i=1}^{C}e^{s\tilde{z_i}}}} \right) #id=nWRQv$

这里的 $\hat{z}$ 表示是由归一化后的特征与权重的内积（即余弦)得到的分数。

Softmax理解之margin

分类模型通过学得的分界线可以表现很不错，但如果要进行特征比对任务，必须将类间的间隔拉得更大，才能保证“类间距离大于类内距离”这一目标（分类与排序的不等价性）。如何提高间隔呢？Margin-based Softmax度量学习可以了解一下，目标是：1️⃣ 除了好的分类概率，一个好的度量空间更加重要；2️⃣ 增大类间差异并且减小类内差异。

输出C个分数，使目标分数比最大的非目标分数更大。

其对应的损失函数为：

$\mathcal{L} = \max( \max_{i\neq y}\{z_i\} - z_y, 0)#id=C7LWo$

参考 hinge loss，引入间隔项：

$\mathcal{L} = \max( \max_{i\neq y}\{z_i\} - z_y + m, 0)#id=lwqHt$

这个损失函数的意义是：

输出C个分数，使目标分数比最大的非目标分数还要大 m。

这里有两个需要注意的问题：一是需要限制分数 $z$ 的取值范围，否则参数 m 设置没有意义，采用一些归一化方法；二是需要控制分数 $z$ 的幅度，保证对目标函数的近似效果和泛化性能，采用尺度因子 s。

于是损失函数变为：

$\mathcal{L} = \max( \max_{i\neq y}\{sz_i\} - sz_y + sm, 0)#id=wrStj$

注意 $max(x,0)$ 的smooth版即softplus函数 $log(1+e^x)$ ，替换后：

$\begin{aligned}
\mathcal{L} &=\max \left(\max _{i \neq y}\left\{s \widetilde{z_{i}}\right\}-s \widetilde{z_{y}}+s m, 0\right) \\
& \approx \operatorname{Softplus}\left(L S E\left(s \widetilde{z_{i}} ; i \neq y\right)-s\left(\widetilde{z_{y}}-m\right)\right) \\
&=-\log \left(\frac{e^{s\left(\widetilde{z_{y}}-m\right)}}{e^{s\left(\widetilde{z_{y}}-m\right)}+\sum_{i \neq y} e^{s \widetilde{z_{i}}}}\right)
\end{aligned}$

这个 loss 也即AM-Softmax loss，“带有加性间隔的 Softmax 交叉熵损失函数”。