Transformer详解          

Transformer

Transformer抛弃了传统的CNN和RNN，整个网络结构完全是由Attention机制组成。更准确地讲，Transformer由且仅由self-Attenion和Feed Forward Neural Network组成。一个基于Transformer的可训练的神经网络可以通过堆叠Transformer的形式进行搭建，作者的实验是通过搭建编码器和解码器各6层，总共12层的Encoder-Decoder，并在机器翻译中取得了BLEU值得新高。

Encoder 结构

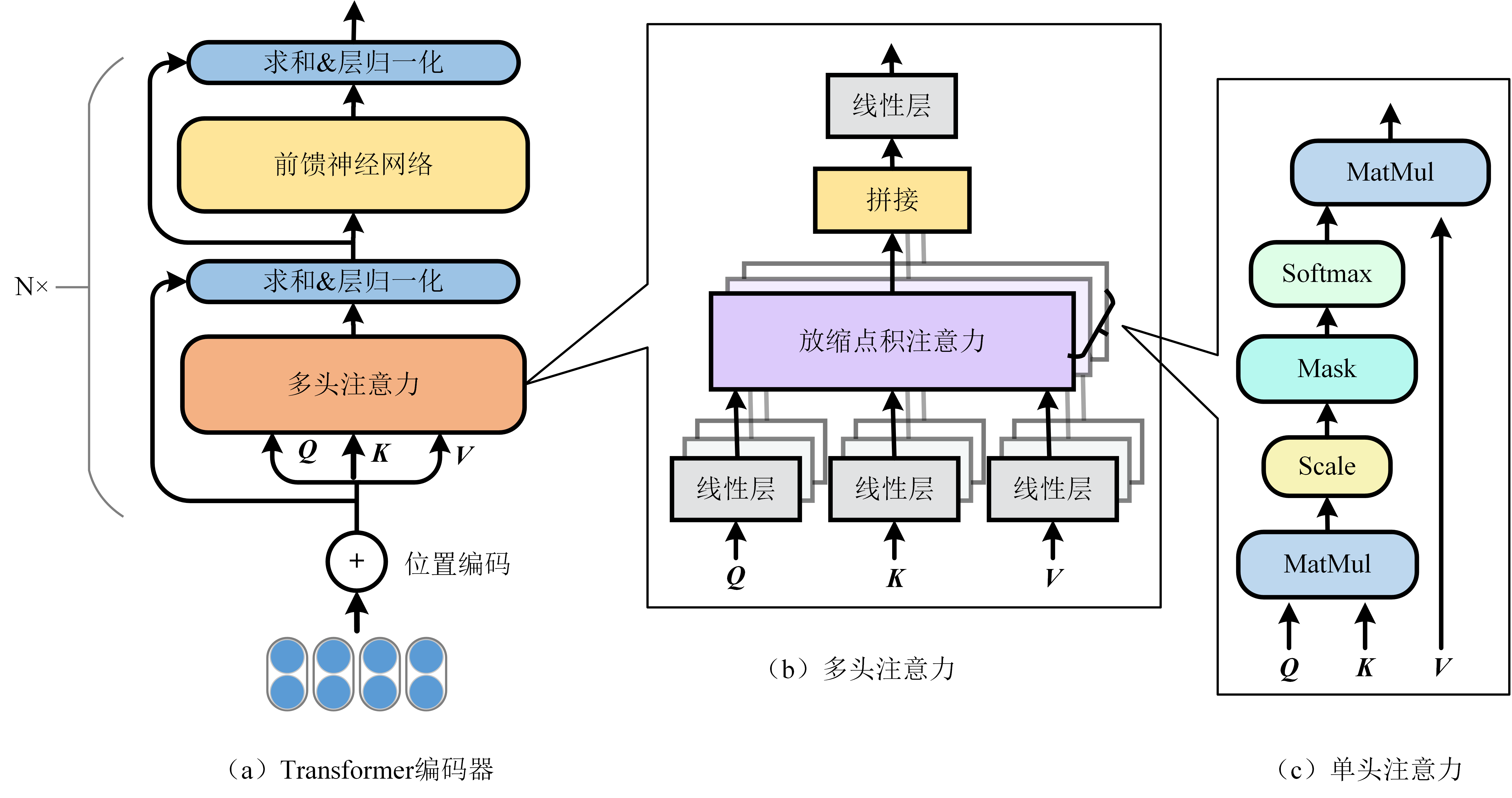
Transformer 包括编码器和解码器两部分。本节主要介绍Transformer的编码器部分，其结构如图2.5（a）所示。它主要包括位置编码（Position Embedding）、多头注意力（Multi-Head Attention）以及前馈神经网络：

Position Embedding

让研究人员绞尽脑汁的Transformer位置编码-科学空间
Transformer Positional Embeddings and Encodings

我们知道，文字的先后顺序，很重要。比如吃饭没、没吃饭、没饭吃、饭吃没、饭没吃，同样三个字，顺序颠倒，所表达的含义就不同了。

不同于RNN、CNN等模型，对于Transformer模型来说，位置编码的加入是必不可少的，因为纯粹的Attention模块是无法捕捉输入顺序的，即无法区分不同位置的Token。为此我们大体有两个选择：1、想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法；2、想办法微调一下Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。

  • 绝对位置编码是相对简单的一种方案，①可以直接将位置编码当作可训练参数，比如最大长度为512，编码维度为768，那么就初始化一个 512×768 的矩阵作为位置向量，让它随着训练过程更新。现在的BERT、GPT等模型所用的就是这种位置编码；②三角函数式位置编码，一般也称为Sinusoidal位置编码，是Google的论文《Attention is All You Need》所提出来的一个显式解，下文会详细介绍；③先接一层RNN学习位置信息，然后再接Transformer，那么理论上就不需要加位置编码了。
    • 输入$x_k$与绝对位置编码$p_k$的组合方式一般是$x_k+p_k$
  • 相对位置并没有完整建模每个输入的位置信息，而是在算Attention的时候考虑当前位置与被Attention的位置的相对距离，由于自然语言一般更依赖于相对位置，所以相对位置编码通常也有着优秀的表现。对于相对位置编码来说，它的灵活性更大，更加体现出了研究人员的“天马行空”。

为了能够对位置信息进行编码，Transformer为序列中的每个单词引入了位置编码特征。通过融合词向量和位置向量，来为每一个词引入了一定的位置信息。Tranformer 采用的是 sin-cos 三角函数式位置编码，计算公式如下：

$\begin{aligned} P E_{(\text {pos}, 2 i)} &=\sin \left(\text {pos} / 10000^{2 i / d}\right) \\ P E_{(\text {pos}, 2 i+1)} &=\cos \left(\text {pos} / 10000^{2 i / d}\right) \end{aligned}$

其中， pos 表示位置编号，目标是将其被映射为一个$d$维的位置向量，该向量的第$i$个元素值通过公式$PE$进行计算。由于$sin(α+β)=sinαcosβ+cosαsinβ$以及$cos(\alpha+\beta)=cos{\alpha}cos{\beta}-sin{\alpha}sin{\beta}$，这表明位置α+β的向量可以表示成位置α和位置β的向量组合，这提供了表达相对位置信息的可能性。但很奇怪的是，现在我们很少能看到直接使用这种形式的绝对位置编码的工作，原因不详。

可以用代码，简单看下效果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 导入依赖库
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import math

def get_positional_encoding(max_seq_len, embed_dim):
    # 初始化一个positional encoding
    # embed_dim: 字嵌入的维度
    # max_seq_len: 最大的序列长度
    positional_encoding = np.array([
        [pos / np.power(10000, 2 * i / embed_dim) for i in range(embed_dim)]
        if pos != 0 else np.zeros(embed_dim) for pos in range(max_seq_len)])
    positional_encoding[1:, 0::2] = np.sin(positional_encoding[1:, 0::2])  # dim 2i 偶数
    positional_encoding[1:, 1::2] = np.cos(positional_encoding[1:, 1::2])  # dim 2i+1 奇数
    # 归一化, 用位置嵌入的每一行除以它的模长
    # denominator = np.sqrt(np.sum(position_enc**2, axis=1, keepdims=True))
    # position_enc = position_enc / (denominator + 1e-8)
    return positional_encoding
    
positional_encoding = get_positional_encoding(max_seq_len=100, embed_dim=16)
plt.figure(figsize=(10,10))
sns.heatmap(positional_encoding)
plt.title("Sinusoidal Function")
plt.xlabel("hidden dimension")
plt.ylabel("sequence length")

Attention层

Attention层的好处是能够**一步到位捕捉到全局的联系**，因为它直接把序列两两比较（代价是计算量变为 $O(n^2)$，当然由于是纯矩阵运算，这个计算量相当也不是很严重）；相比之下，RNN需要一步步递推才能捕捉到，而CNN则需要通过层叠来扩大感受野，这是Attention层的明显优势。

Self Attention 具体操作如下：首先，每个词都要通过三个矩阵Wq, Wk, Wv进行一次线性变化，一分为三，生成每个词自己的query, key, vector三个向量。以一个词为中心进行Self Attention时，都是用这个词的key向量与每个词的query向量做点积，再通过Softmax归一化出权重。然后通过这些权重算出所有词的vector的加权和，作为这个词的输出。

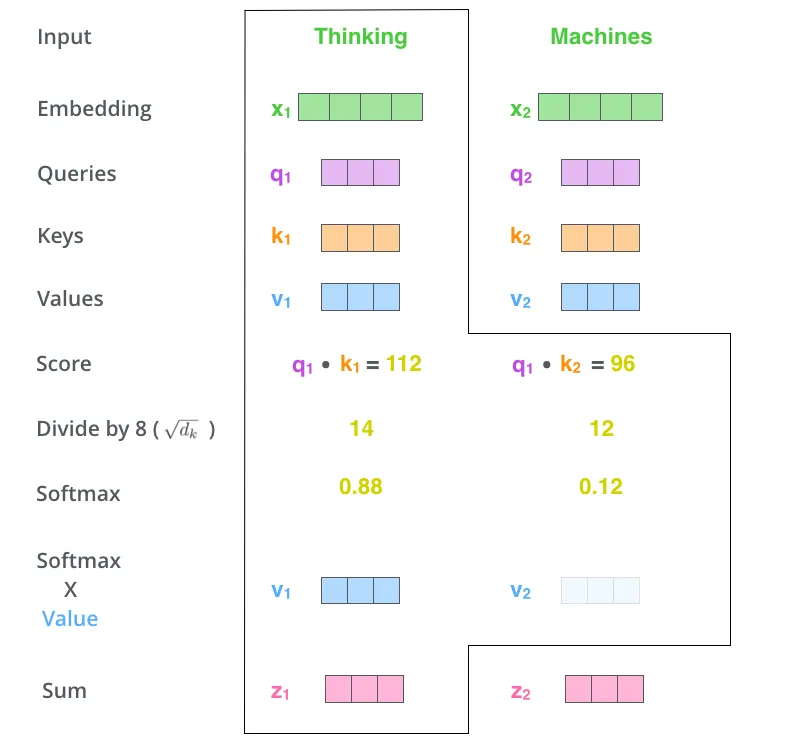
Google给出的Attention的定义:

${Attention}(Q, K, V)=softmax(\frac{QK^T}{\sqrt{d_k}})V$

其中，$\boldsymbol{Q} \in \mathbb{R}^{n \times d{k}}, \boldsymbol{K} \in \mathbb{R}^{m \times d{k}}, \boldsymbol{V} \in \mathbb{R}^{m \times d_{v}} , Z是归一化因子$。单头注意力通过「放缩点积注意力」（Scaled dot-product attention）来将查询$Q$与$K$进行点积并缩放，再馈送到Softmax函数以获得与$V$对应的相似度权重。根据这些权重对序列自身$V$进行加权求和，建模序列内部联系，从而得到$n$个$d$维的输出向量。其中因子$\sqrt{d_k}$起到调节作用，使得内积不至于太大（太大的话softmax后就非0即1了，不够“soft”了）。

逐个向量来看:

$Attention \left(\boldsymbol{q}_{t}, \boldsymbol{K}, \boldsymbol{V}\right)=\sum_{s=1}^{m} \frac{1}{Z} \exp \left(\frac{\left\langle\boldsymbol{q}_{t}, \boldsymbol{k}_{s}\right\rangle}{\sqrt{d_{k}}}\right) \boldsymbol{v}_{s}$

其中，$q,k,v$ 分别是 $query,key,value$ 的简写。

最终Self Attention将$n×d_k$的输入序列$Q$编码成了一个新的$n×dv$的输出序列.

小结：所谓Self Attention，其实就是$Attention(X,X,X)$，$X$ 就是前面说的输入序列。也就是说，在序列内部做Attention，寻找序列内部的联系。

Multi-Head Attention

所谓“多头”指的是同样的操作（参数不共享）重复多遍，然后把结果拼接起来。多头注意力的结构如图2.5（b）所示，把$Q,K,V$通过参数矩阵映射一下，然后做单头注意力（自注意力），把这个过程重复做 $h$ 次，结果拼接起来，最后得到一个 $n×(hd_v)$ 的序列。

${head}_{i} = {Attention}(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V})
\\
{MultiHead}(Q, K, V) ={Concat}({head}_{1}, \cdots, {head}_{h})$

其中，$W^Q,W^K,W^V$ 对应线性变换的权重矩阵。

Add & Norm 层

Add表示残差，将一层的输入与其标准化后的输出进行相加即可。Norm表示层归一化（Layer Normalization），具体可看《归一化方法介绍》

前馈神经网络FFN

序列经过Add & Norm层后，会被送入 FFN层 中进行降维处理。前馈神经网络包含两个线性变换和一个非线性ReLU激活函数，计算公式如下：

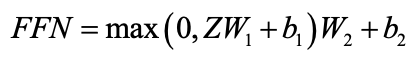
其中，$W_1,W_2,b_1,b_2$ 是可训练的参数。

Decoder 结构

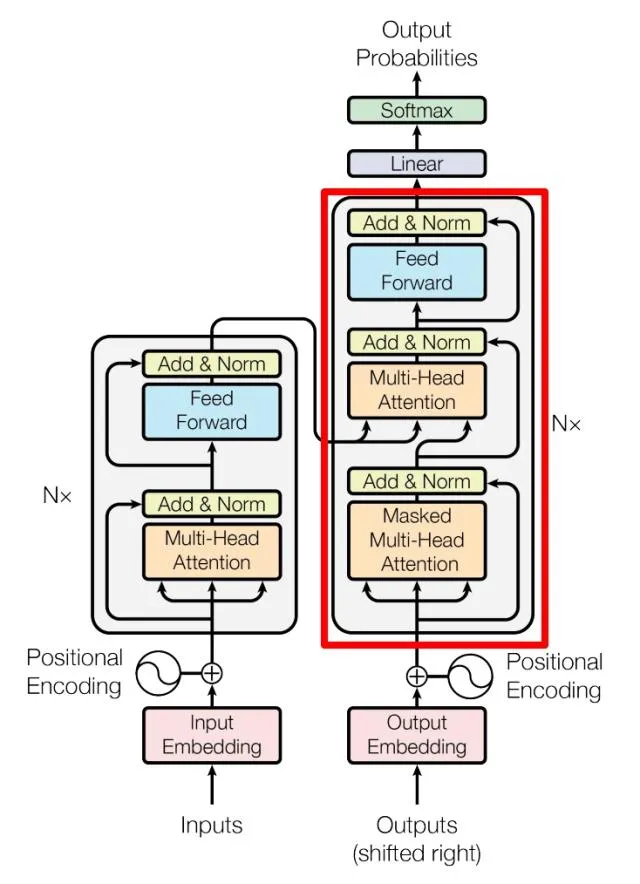
基于 transformer-decoder 的 CLM 是如何工作的？

Transformer Decoder block

上图红色部分为 Transformer 的 Decoder block 结构，与 Encoder block 相似，但是存在一些区别：

  • 包含两个 Multi-Head Attention 层。
  • 第一个 Multi-Head Attention 层采用了 Masked 操作。
  • 第二个 Multi-Head Attention 层的K, V矩阵使用 Encoder 的编码信息矩阵C进行计算，而Q使用上一个 Decoder block 的输出计算。
  • 最后有一个 Softmax 层计算下一个翻译单词的概率。

5.1 第一个 Multi-Head Attention

Decoder block 的第一个 Multi-Head Attention 采用了 Masked 操作，因为在翻译的过程中是顺序翻译的，即翻译完第 i 个单词，才可以翻译第 i+1 个单词。通过 Masked 操作可以防止第 i 个单词知道 i+1 个单词之后的信息。下面以 “我有一只猫” 翻译成 “I have a cat” 为例，了解一下 Masked 操作。

下面的描述中使用了类似 Teacher Forcing 的概念，不熟悉 Teacher Forcing 的童鞋可以参考以下上一篇文章Seq2Seq 模型详解。在 Decoder 的时候，是需要根据之前的翻译，求解当前最有可能的翻译，如下图所示。首先根据输入 ““ 预测出第一个单词为 “I”，然后根据输入 “ I” 预测下一个单词 “have”。

Decoder 预测

Decoder 可以在训练的过程中使用 Teacher Forcing 并且并行化训练，即将正确的单词序列 ( I have a cat) 和对应输出 (I have a cat ) 传递到 Decoder。那么在预测第 i 个输出时，就要将第 i+1 之后的单词掩盖住，注意 Mask 操作是在 Self-Attention 的 Softmax 之前使用的，下面用 0 1 2 3 4 5 分别表示 “ I have a cat “。

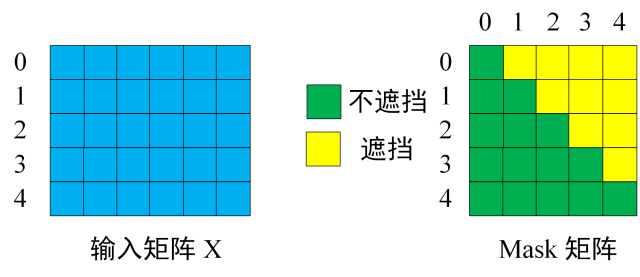
第一步：是 Decoder 的输入矩阵和 Mask 矩阵，输入矩阵包含 “ I have a cat” (0, 1, 2, 3, 4) 五个单词的表示向量，Mask 是一个 5×5 的矩阵。在 Mask 可以发现单词 0 只能使用单词 0 的信息，而单词 1 可以使用单词 0, 1 的信息，即只能使用之前的信息。

输入矩阵与 Mask 矩阵

第二步：接下来的操作和之前的 Self-Attention 一样，通过输入矩阵X计算得到Q,K,V矩阵。然后计算Q和 $K^T$ 的乘积 $QK^T$ 。

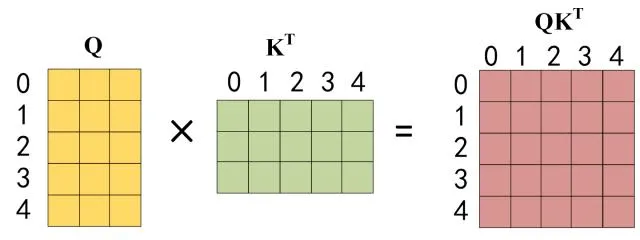
Q乘以K的转置

第三步：在得到 $QK^T$ 之后需要进行 Softmax，计算 attention score，我们在 Softmax 之前需要使用Mask矩阵遮挡住每一个单词之后的信息，遮挡操作如下：

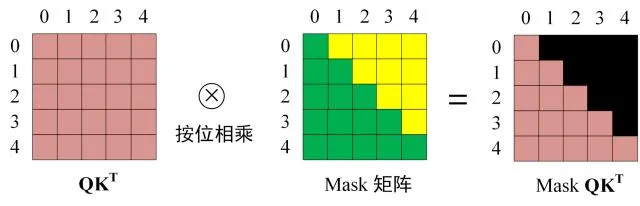
Softmax 之前 Mask

得到 Mask $QK^T$ 之后在 Mask $QK^T$上进行 Softmax，每一行的和都为 1。但是单词 0 在单词 1, 2, 3, 4 上的 attention score 都为 0。

第四步：使用 Mask $QK^T$与矩阵 V相乘，得到输出 Z，则单词 1 的输出向量 $Z_1$ 是只包含单词 1 信息的。

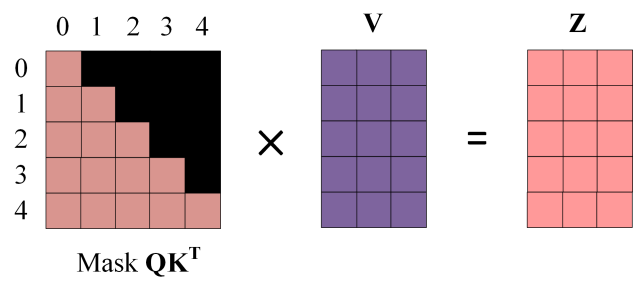
Mask 之后的输出

第五步：通过上述步骤就可以得到一个 Mask Self-Attention 的输出矩阵 $Z_i$ ，然后和 Encoder 类似，通过 Multi-Head Attention 拼接多个输出Zi 然后计算得到第一个 Multi-Head Attention 的输出Z，Z与输入X维度一样。

5.2 第二个 Multi-Head Attention

Decoder block 第二个 Multi-Head Attention 变化不大， 主要的区别在于其中 Self-Attention 的 K, V矩阵不是使用 上一个 Decoder block 的输出计算的，而是使用 Encoder 的编码信息矩阵 C 计算的。

根据 Encoder 的输出 C计算得到 K, V，根据上一个 Decoder block 的输出 Z 计算 Q (如果是第一个 Decoder block 则使用输入矩阵 X 进行计算)，后续的计算方法与之前描述的一致。

这样做的好处是在 Decoder 的时候，每一位单词都可以利用到 Encoder 所有单词的信息 (这些信息无需 Mask)。

5.3 Softmax 预测输出单词

Decoder block 最后的部分是利用 Softmax 预测下一个单词，在之前的网络层我们可以得到一个最终的输出 Z，因为 Mask 的存在，使得单词 0 的输出 Z0 只包含单词 0 的信息，如下：

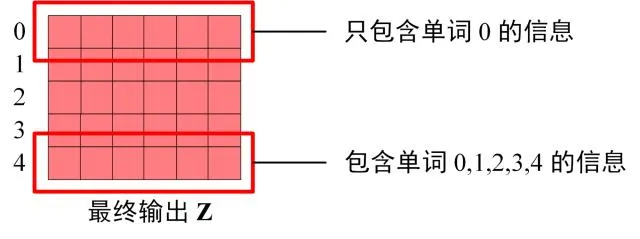
Decoder Softmax 之前的 Z

Softmax 根据输出矩阵的每一行预测下一个单词：

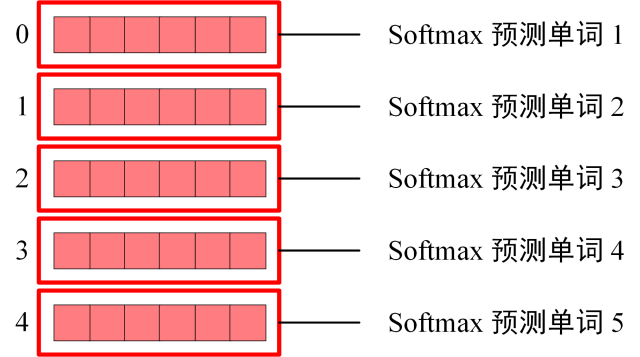
Decoder Softmax 预测

这就是 Decoder block 的定义，与 Encoder 一样，Decoder 是由多个 Decoder block 组合而成。

Transformer 总结

  1. Transformer摆脱了nlp任务对于rnn，lstm的依赖，在长距离上的建模能力更强；
  2. 使用了 self-attention 可以并行化地对上下文进行建模，提高了训练和推理的速度；
  3. Transformer 本身是不能利用单词的顺序信息的，因此需要在输入中添加位置 Embedding，否则 Transformer 就是一个词袋模型了。
  4. Transformer 的重点是 Self-Attention 结构，其中用到的 Q, K, V矩阵通过输出进行线性变换得到。
  5. Transformer 中 Multi-Head Attention 中有多个 Self-Attention，可以捕获单词之间多种维度上的相关系数 attention score。
  6. Transformer也是后续更强大的nlp预训练模型的基础（bert系列使用了transformer的encoder，gpt系列transformer的decoder）

参考

llm
#Transformer
Transformer详解          
http://example.com/2023/02/26/2023-02-26-Transformer详解/
作者
BY NSX                  # 作者
发布于
2023年2月26日
许可协议