PPO算法

要点

  • 根据 OpenAI 的官方博客, PPO 已经成为他们在强化学习上的默认算法. 如果一句话概括 PPO: OpenAI 提出的一种解决 Policy Gradient 不好确定 Learning rate (或者 Step size) 的问题. 因为如果 step size 过大, 学出来的 Policy 会一直乱动, 不会收敛, 但如果 Step Size 太小, 对于完成训练, 我们会等到绝望. PPO 利用 New Policy 和 Old Policy 的比例, 限制了 New Policy 的更新幅度, 让 Policy Gradient 对稍微大点的 Step size 不那么敏感.
  • 总的来说 PPO 是一套 Actor-Critic 结构, Actor 想最大化 J_PPO, Critic 想最小化 L_BL.

PG Add Constraint → PPO

简单来说，PPO就是Policy Gradient的”off-policy”版本。为了满足Importance Sampling的使用条件，即防止$p_{\theta}$和$p_{\theta_{old}}$两个概率分布相差太多，PPO提供了两个解决方案：

  1. TRPO（Trust Region Policy Optimization）在目标函数外使用KL Penalty (惩罚项）来限制策略更新，希望在训练的过程中，new Policy 和 old Policy 的输出不要相差太大（因为输出的 action 是概率分布，也即计算两个概率分布之间的差别）。但是这种方法实现起来很复杂，需要更多的计算时间。

$L^{PPO}(\theta)=E_{t}\left[r_t(\theta) * A_{t}\right]-\beta·KL[\pi_{\theta_{init}}|\pi_{\theta}]$

  1. PPO-Clip 在目标函数中使用 Clipped surrogate objective function 来直接裁剪概率比率。所要做的事情本质上和TRPO是一样的，都是为了让两个分布（$θ$和$θ’$）之间的差距不致过大

$L^{C L I P}(\theta)=\hat{\mathbb{E}}_{t}\left[\min \left(r_{t}(\theta) \hat{A}_{t}, \operatorname{clip}\left(r_{t}(\theta), 1-\epsilon, 1+\epsilon\right) \hat{A}_{t}\right)\right]$

其中，$\beta$是可以动态调整的，称之为自适应KL惩罚（adaptive KL penalty）；$r_t(\theta)$表示Ratio Function，指产生同样的 token，在 Policy Model 和 Alignment Model 下的概率比值（It’s the probability of taking action a_t at state s_t in the current policy divided by the previous one. ）

$r_t(\theta)=\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$

正如我们所看到的，$r_t(\theta)$表示当前策略和旧策略之间的概率比率，是估计旧策略和当前策略之间差异的一种简单方法。

  • 如果$r_t(\theta)>1$，则在状态$s_t$下，动作$a_t$在当前策略中比旧策略更有可能执行。
  • 如果$0<r_t(\theta)<1$，则在当前策略下执行该动作的可能性比旧策略下低。

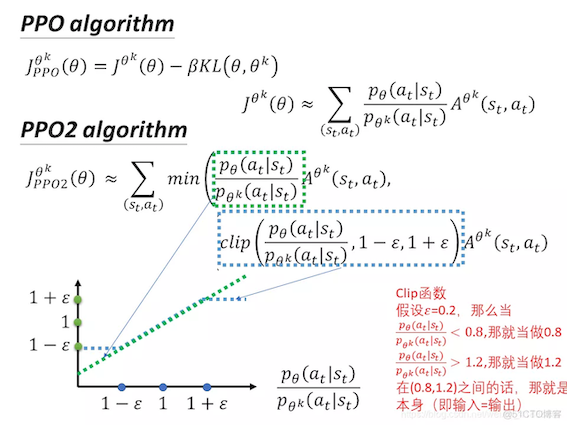
PPO-Clip 算法直观理解

$L^{C L I P}(\theta)=\hat{\mathbb{E}}_{t}\left[\min \left(r_{t}(\theta) \hat{A}_{t}, \operatorname{clip}\left(r_{t}(\theta), 1-\epsilon, 1+\epsilon\right) \hat{A}_{t}\right)\right]$
$r_t(\theta)=\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}$

整个目标函数在$min$这个大括号里有两部分，最终对比两部分哪部分更小，就取哪部分的值。
在括号的第二部分中，

  • 首先是裁剪函数$clip$：如果$p_{\theta}(a_t|s_t)$和$p_{\theta^k}(a_t|s_t)$之间的概率比落在范围$(1-ε)$和$(1+ε)$之外，$\frac{p_{\theta}(a_t|s_t)}{p_{\theta^k}(a_t|s_t)}$将被剪裁，使得其值最小不小于$(1-ε)$，最大不大于$(1+ε)$
  • 然后是$clip$括号外乘以$A^{\theta’}(s_t,a_t)$：当$A>0$，则说明这是好动作，那么希望增大这个action的几率$p_{\theta}(a_t|s_t)$，但是又不希望两者差异，即比值$\frac{p_{\theta}(a_t|s_t)}{p_{\theta^k}(a_t|s_t)}$太悬殊，所以增大到比值为$1+ε$就不要再增加了；当$A<0$，则说明该动作不是好动作，那么希望这个action出现的几率$p_{\theta}(a_t|s_t)$越小越好，但$\frac{p_{\theta}(a_t|s_t)}{p_{\theta^k}(a_t|s_t)}$最小不能小过$(1-ε)$

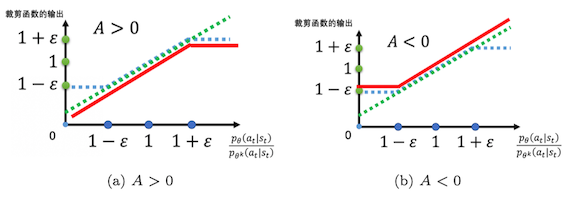
换言之，这个裁剪算法和KL散度约束所要做的事情本质上是一样的，都是为了让两个分布之间的差距不致过大，但裁剪算法相对好实现，别看看起来复杂，其实代码很好写，示例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// ratios即为重要性权重
// 括号里的environment_log_probs代表用于与环境交互的策略
ratios = torch.exp(log_probs - environment_log_probs)
 
// 分别用sur_1、sur_2来计算公式的两部分

// 第一部分是重要性权重乘以优势函数
sur_1 = ratios * advs
 
// 第二部分是具体的裁剪过程
sur_2 = torch.clamp(ratios, 1 - clip_eps, 1 + clip_eps) * advs
 
// 最终看谁更小则取谁
clip_loss = -torch.min(sur_1,sur_2).mean()

简单 PPO 的代码解读

https://mofanpy.com/tutorials/machine-learning/reinforcement-learning/DPPO

我们用 Tensorflow 搭建神经网络, tensorboard 中可以看清晰的看到我们是如果搭建的:

图中的 pi 就是我们的 Actor 了. 每次要进行 PPO 更新 Actor 和 Critic 的时候, 我们有需要将 pi 的参数复制给 oldpi. 这就是 update_oldpi 这个 operation 在做的事. Critic 和 Actor 的内部结构, 我们不会打开细说了. 因为就是一堆的神经网络而已. 这里的 Actor 使用了 normal distribution 正态分布输出动作.

这个 PPO 我们可以用一个 Python 的 class 代替:

1
2
3
4
5
6
7
8
9
10
class PPO(object):
    def __init__(self):
        # 建 Actor Critic 网络
        # 搭计算图纸 graph
    def update(self, s, a, r):
        # 更新 PPO
    def choose_action(self, s):
        # 选动作
    def get_v(self, s):
        # 算 state value

而这个 PPO 和 env 环境的互动可以简化成这样.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
ppo = PPO()
for ep in range(EP_MAX):
    s = env.reset()
    buffer_s, buffer_a, buffer_r = [], [], []
    for t in range(EP_LEN):
        env.render()
        a = ppo.choose_action(s)
        s_, r, done, _ = env.step(a)
        buffer_s.append(s)
        buffer_a.append(a)
        buffer_r.append((r+8)/8)    # normalize reward, 发现有帮助
        s = s_

        # 如果 buffer 收集一个 batch 了或者 episode 完了
        if (t+1) % BATCH == 0 or t == EP_LEN-1:
            # 计算 discounted reward
            v_s_ = ppo.get_v(s_)
            discounted_r = []
            for r in buffer_r[::-1]:
                v_s_ = r + GAMMA * v_s_
                discounted_r.append(v_s_)
            discounted_r.reverse()

            bs, ba, br = batch(buffer_s, buffer_a, discounted_r)
            # 清空 buffer
            buffer_s, buffer_a, buffer_r = [], [], []
            ppo.update(bs, ba, br)  # 更新 PPO

了解了这些更新步骤, 我们就来看看如何更新我们的 PPO. 我们更新 Critic 的时候是根据 刚刚计算的 discounted_r 和自己分析出来的 state value 这两者的差 (advantage). 然后最小化这个差值:

1
2
3
4
5
6
class PPO:
    def __init__(self):
        self.advantage = self.tfdc_r - self.v   # discounted reward - Critic 出来的 state value
        self.closs = tf.reduce_mean(tf.square(self.advantage))
        self.ctrain_op = tf.train.AdamOptimizer(C_LR).minimize(self.closs)

两种更新 Actor 的方式 KL penalty 和 clipped surrogate objective

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class PPO:
    def __init__(self):
        self.tfa = tf.placeholder(tf.float32, [None, A_DIM], 'action')
        self.tfadv = tf.placeholder(tf.float32, [None, 1], 'advantage')
        with tf.variable_scope('loss'):
            with tf.variable_scope('surrogate'):
                ratio = pi.prob(self.tfa) / oldpi.prob(self.tfa)
                surr = ratio * self.tfadv   # surrogate objective
            if METHOD['name'] == 'kl_pen':      # 如果用 KL penatily
                self.tflam = tf.placeholder(tf.float32, None, 'lambda')
                kl = kl_divergence(oldpi, pi)
                self.kl_mean = tf.reduce_mean(kl)
                self.aloss = -(tf.reduce_mean(surr - self.tflam * kl))
            else:                               # 如果用 clipping 的方式
                self.aloss = -tf.reduce_mean(tf.minimum(
                    surr,
                    tf.clip_by_value(ratio, 1.-METHOD['epsilon'], 1.+METHOD['epsilon'])*self.tfadv))

        with tf.variable_scope('atrain'):
            self.atrain_op = tf.train.AdamOptimizer(A_LR).minimize(self.aloss)

好了, 接下来就是最重要的更新 PPO 时间了, 同样, 如果觉得我这些代码省略的很严重, 请直接前往我的 Github 看全套代码. 注意的是, 这个 update 的步骤里, 我们用 for loop 更新了很多遍 Actor 和 Critic, 在 loop 之前, pi 和 old pi 是一样的, 每次 loop 的之后, pi 会变动, 而 old pi 不变, 这样这个 surrogate 就会开始变动了. 这就是 PPO 的精辟.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class PPO:
    def update(self, s, a, r):
        # 先要将 oldpi 里的参数更新 pi 中的
        self.sess.run(self.update_oldpi_op)

        # 更新 Actor 时, kl penalty 和 clipping 方式是不同的
        if METHOD['name'] == 'kl_pen':  # 如果用 KL penalty
            for _ in range(A_UPDATE_STEPS):
                _, kl = self.sess.run(
                        [self.atrain_op, self.kl_mean],
                        {self.tfs: s, self.tfa: a, self.tfadv: adv, self.tflam: METHOD['lam']})
                # 之后根据 kl 的值, 调整 METHOD['lam'] 这个参数
        else:   # 如果用 clipping 的方法
            [self.sess.run(self.atrain_op, {self.tfs: s, self.tfa: a, self.tfadv: adv}) for _ in range(A_UPDATE_STEPS)]

        # 更新 Critic 的时候, 他们是一样的
        [self.sess.run(self.ctrain_op, {self.tfs: s, self.tfdc_r: r}) for _ in range(C_UPDATE_STEPS)]

最后我们看一张学习的效果图:

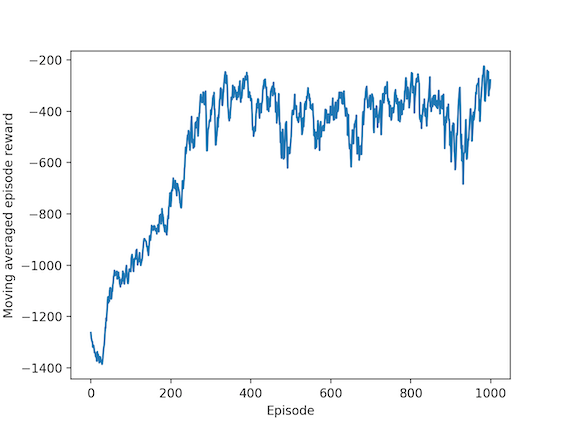
好了这就是整个 PPO 的主要流程了, 其他的步骤都没那么重要了, 可以直接在我的 Github 看全套代码 中轻松弄懂.

PPO Actor-Critic Loss

PPO Actor-Critic 风格的最终 Clipped Surrogate Objective Loss 看起来像这样，它是 Clipped Surrogate Objective 函数、Value Loss Function 和 Entropy bonus 的组合：

DeepMind 总结 OpenAI conference 上的 PPO 的伪代码

参考

李宏毅老师的深度强化学习课程
Unit 8. Introduction to PPO - Hugging Face
图解人工反馈强化学习(RLHF) - Hugging Face

强化学习
#PPO
PPO算法
http://example.com/2023/03/14/PPO算法/
作者
Ning Shixian
发布于
2023年3月14日
许可协议